ЬтФПФкШн
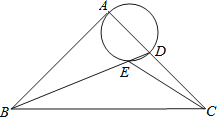
ЁОЬтФПЁПНшМјЮвУЧвбгабаОПКЏЪ§ЕФОбщЃЌЬНЫїКЏЪ§![]() ЕФЭМЯѓгыаджЪЃЌЬНОПЙ§ГЬШчЯТЃЌЧыВЙГфЭъећ.
ЕФЭМЯѓгыаджЪЃЌЬНОПЙ§ГЬШчЯТЃЌЧыВЙГфЭъећ.
ЃЈ1ЃЉздБфСП![]() ЕФШЁжЕЗЖЮЇЪЧШЋЬхЪЕЪ§ЃЌ
ЕФШЁжЕЗЖЮЇЪЧШЋЬхЪЕЪ§ЃЌ![]() гы
гы![]() ЕФМИзщЖдгІжЕСаБэШчЯТЃК
ЕФМИзщЖдгІжЕСаБэШчЯТЃК
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЦфжаЃЌ![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
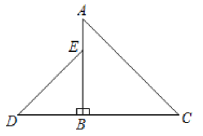
ЃЈ2ЃЉИљОнЩЯБэЪ§ОнЃЌдкШчЭМЫљЪОЕФЦНУцжБНЧзјБъЯЕжаУшЕуЃЌВЂЛГіКЏЪ§ЭМЯѓЃЛ

ЃЈ3ЃЉЙлВьКЏЪ§ЭМЯѓЃК
ЂйЕБЗНГЬ![]() гаЧвНігаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌИљОнКЏЪ§ЭМЯѓжБНгаДГі
гаЧвНігаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌИљОнКЏЪ§ЭМЯѓжБНгаДГі![]() ЕФШЁжЕЗЖЮЇЮЊ ЃЛ
ЕФШЁжЕЗЖЮЇЮЊ ЃЛ
ЂкдкИУЦНУцжБНЧзјБъЯЕжаЛГіжБЯп![]() ЕФЭМЯѓЃЌИљОнЭМЯѓжБНгаДГіИУжБЯпгыКЏЪ§
ЕФЭМЯѓЃЌИљОнЭМЯѓжБНгаДГіИУжБЯпгыКЏЪ§![]()
![]() ЕФНЛЕуКсзјБъЮЊЃК ЃЈНсЙћБЃСєвЛЮЛаЁЪ§ЃЉ.
ЕФНЛЕуКсзјБъЮЊЃК ЃЈНсЙћБЃСєвЛЮЛаЁЪ§ЃЉ.
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЌ
ЃЌ![]() ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉЂй
ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉЂй![]() Лђ
Лђ![]() ЃЛЂк
ЃЛЂк![]() ЃЌ
ЃЌ![]()
ЁОНтЮіЁП
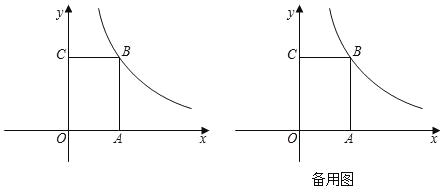
ЃЈ1ЃЉАбx=-2КЭx=1,ДњШыБэДяЪНМДПЩЧѓНтЃЛ
ЃЈ2ЃЉИљОнБэИёжаЕФЪ§ОндкжБНЧШ§НЧаЮУшЕуСЌЯпМДПЩЃЛ
ЃЈ3ЃЉЂйИљОн![]() =b,евЕНКЏЪ§гыy=b,гаСНИіНЛЕуЕФЧщПіМДПЩЧѓНт.
=b,евЕНКЏЪ§гыy=b,гаСНИіНЛЕуЕФЧщПіМДПЩЧѓНт.
ЂкИљОнжБНЧзјБъЯЕжаСНКЏЪ§ЕФНЛЕуЕФКсзјБъМДПЩЧѓНт.
ЃЈ1ЃЉx=-2ЪБЃЌy=3ЃЌ
ЕБx=1ЃЌy=2,
ЙЪЬюЃК3ЃЛ2ЃЛ
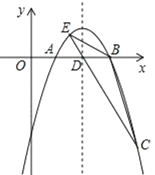
ЃЈ2ЃЉЭМЯѓШчЯТЃК

ЃЈ3ЃЉЂйСю![]() =b,
=b,
ЙЪевЕНКЏЪ§гыy=b,гаСНИіНЛЕуЕФЧщПіМДПЩ
гЩЭМЯёПЩжЊb=-2ЛђbЃО2ЪБКЏЪ§![]() гыy=bгаСНИіНЛЕуЃЌ
гыy=bгаСНИіНЛЕуЃЌ
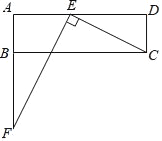
ЙЪЗНГЬ![]() гаЧвНігаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌГі
гаЧвНігаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌГі![]() ЕФШЁжЕЗЖЮЇЮЊ
ЕФШЁжЕЗЖЮЇЮЊ![]() Лђ
Лђ![]() ЃЛ
ЃЛ
ЂкШчЭМЃЌЛГіжБЯп![]() ЕФЭМЯѓЃЌИљОнЭМЯёМДПЩевЕНжБЯпгыКЏЪ§
ЕФЭМЯѓЃЌИљОнЭМЯёМДПЩевЕНжБЯпгыКЏЪ§![]()
![]() ЕФНЛЕуКсзјБъЮЊ
ЕФНЛЕуКсзјБъЮЊ![]() КЭ
КЭ![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊ![]() КЭ
КЭ![]() .
.