Question

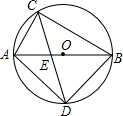如图，⊙O直径AB为5cm，弦AC为3cm，∠ACB的平分线交⊙O于D，求BC、AD、BD的长．

Answer 1

分析：根据题意可得出△ABC，△ABD是直角三角形，再根据勾股定理得出BC，根据等弧所对的圆周角相等可得出AD=BD，即可求出BD．

解答：解：∵⊙O直径AB为5cm，
∴∠ACB=∠ADB=90°，
∵弦AC为3cm，
∴BC=4cm，
∵∠ACB的平分线交⊙O于D，
∴

AD

=

BD

，
∴AD=BD，
∴在Rt△ADB中，AD²+BD²=AB²，
∵AB=5cm，
∴AD=BD=

5 2

2

cm．

点评：本题考查了等腰直角三角形、圆周角定理以及勾股定理，是基础知识比较简单．