题目内容

如图，在⊙O中，弦AB∥弦CD，且分居在点O的两侧．已知AB=11，CD=21，⊙O的半径R=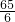 $数学公式$ ．求：

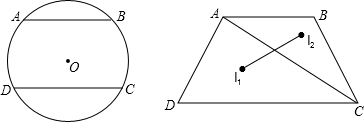
（1）AB与CD之间的距离．
（2）若⊙I₁、⊙I₂分别为△ACD、△ABC的内切圆，求⊙I₁、⊙I₂的半径之比．

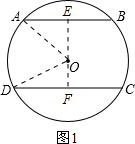解：（1）如图1，过O作OE⊥AB于点E，OF⊥CD于点F，连接OA，OD．
∵AB∥CD，∴E，O，F三点共线，
∴EF即为所求的AB，CD的距离
∴AE= $\text{[math]}$ AB= $\text{[math]}$ ，DF= $\text{[math]}$ CD= $\text{[math]}$ ，
在Rt△OAE中，∵OB= 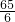$\text{[math]}$ ，AE= $\text{[math]}$ ，∴OE= $\text{[math]}$ ．
在Rt△ODF中，∵OD= 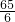$\text{[math]}$ ，DF= $\text{[math]}$ ，∴OF= $\text{[math]}$ ，
∴EF=OE+OF= $\text{[math]}$ + $\text{[math]}$ =12，
答：AB和CD的距离为12；

（2）∵AB∥CD，AB≠CD，
∴四边形ABCD是梯形，
∵在⊙O中，弦AB∥弦CD，
∴ $\text{[math]}$ = $\text{[math]}$ ，
∴AD=BC，
∴梯形ABCD是等腰梯形．
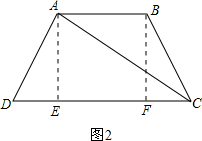
如图2，作等腰梯形ABCD的高AE，BF，则四边形ABFE是矩形，FE=AB=11，DE=CF= 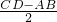$\text{[math]}$ =5．
在△ADE中，∵∠AED=90°，
∴AD= 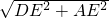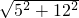$\text{[math]}$ = $\text{[math]}$ =13，
在△ACE中，∵∠AEC=90°，
∴AC= 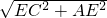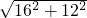$\text{[math]}$ = $\text{[math]}$ =20．
S_梯形ABCD= $\text{[math]}$ （AB+CD）•EF= $\text{[math]}$ （11+21）×12=192，
∵S_△ADC+S_△ABC=192，S_△ADC：S_△ABC=21：11，
∴S_△ADC=126，S_△ABC=66．

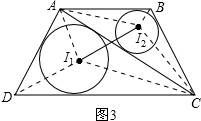如图3，连接I₁A、I₁D、I₁C，设△ACD的内切圆半径为r₁，
∵S_△ADC=S_△AI1D+S_△DI1C+S_△AI1C= $\text{[math]}$ AD•r₁+ $\text{[math]}$ CD•r₁+ $\text{[math]}$ CA•r₁，
∴ $\text{[math]}$ （13+21+20）r₁=126，
∴r₁= $\text{[math]}$ ，
同理，求出⊙I₂的半径r₂=3，
∴⊙I₁与⊙I₂的半径之比是 $\text{[math]}$ ：3= $\text{[math]}$ ．
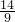分析：（1）分别作弦AB、CD的弦心距，设垂足为E、F；由于AB∥CD，则E、O、F三点共线，EF即为AB、CD间的距离；由垂径定理，易求得AE、DF的长，连接OA、OD，在构建的直角三角形中，根据勾股定理即可求出OE、OF的长，也就求出了EF的长，即弦AB、CD间的距离；
（2）先证明四边形ABCD是等腰梯形，作等腰梯形ABCD的高AE，BF，运用勾股定理求出AD=13，AC=20，运用梯形的面积公式得出S_梯形ABCD=192，则S_△ADC=126，S_△ABC=66，然后由面积法分别求出⊙I₁的半径r₁= $\text{[math]}$ ，⊙I₂的半径r₂=3，则⊙I₁与⊙I₂的半径之比可求．
点评：本题考查了等腰梯形的判定与性质，垂径定理，勾股定理，三角形的内切圆，三角形、梯形的面积，综合性较强，有一定难度．