题目内容
【题目】如图，
的
、
的平分线
、
相交于点
，求证：
.
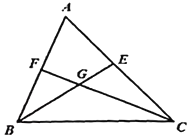
【答案】见解析
【解析】
先根据△ABC的∠B和∠C的平分线BE，CF交于点G得出∠1=∠2=
∠ABC，∠3=∠4=∠ACB，再由三角形内角和定理得出∠ABC+∠ACB=180°-∠A，进而可得出∠2+∠4=90°-∠A，由∠BGC+（∠2+∠4）=180°即可得出结论．
∵△ABC的∠B和∠C的平分线BE，CF交于点G，
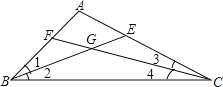
∴∠1=∠2=∠ABC，∠3=∠4=∠ACB，
∵∠A+∠ABC+∠ACB=180°，
∴∠ABC+∠ACB=180°-∠A，
∴（∠ABC+∠ACB）=90°-∠A，即∠2+∠4=90°-∠A，
∵∠BGC+（∠2+∠4）=180°，
∴∠BGC=180°-（∠2+∠4）=180°-（90°-∠A）=90°+∠A．
练习册系列答案
相关题目
