Question

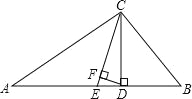
【题目】如图，在Rt△ABC中，∠ABC＝90，AB＝BC＝，将△ABC绕点A逆时针旋转60，得到△ADE，连接BE，则BE的长是_________

Answer 1

【答案】

【解析】

首先考虑到BE所在的三角形并不是特殊三角形，所以猜想到要求BE，可能需要构造直角三角形．由旋转的性质可知，AC=AE，∠CAE=60°，故△ACE是等边三角形，可证明△ABE与△CBE全等，可得到∠ABE=45°，∠AEB=30°，再证△AFB和△AFE是直角三角形，然后在根据勾股定理求解．

连结CE，设BE与AC相交于点F，如图所示．

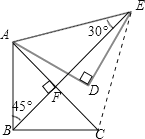
∵Rt△ABC中，AB=BC，∠ABC=90°，∴∠BCA=∠BAC=45°．

∵AB=BC=，∴AC==4．

∵Rt△ABC绕点A逆时针旋转60°与Rt△ADE重合，∴∠BAC=∠DAE=45°，AC=AE．

又∵旋转角为60°，∴∠BAD=∠CAE=60°，∴△ACE是等边三角形，∴AC=CE=AE=4．

在△ABE与△CBE中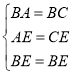，∵，∴△ABE≌△CBE（SSS），∴∠ABE=∠CBE=45°，∠CEB=∠AEB=30°，∴∠BFA=180°﹣45°﹣45°=90°，∴∠AFB=∠AFE=90°．

在Rt△ABF中，由勾股定理得：BF=AF2．

又在Rt△AFE中，∠AEF=30°，∠AFE=90°，FEAF=2，∴BE=BF+FE=．

故答案为：．