Question

已知反比例函数y=

m-8

x

（m为常数）的图象经过点A（-1，6）．如图，过点A作直线AC与函数y=

m-8

x

的图象交于点B，与x轴交于点C，且AB=2BC，则点C的坐标为（　　）

• A、（-3，0）
• B、（-4，0）
• C、（-5，0）
• D、（-6，0）

Answer 1

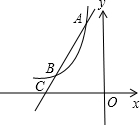
分析：将A点坐标代入反比例函数解析式即可得到一个关于m的一元一次方程，求出m的值；再分别过点A、B作x轴的垂线，垂足分别为点E、D，则△CBD∽△CAE，运用相似三角形知识求出CD的长即可求出点C的横坐标．

解答：解：∵图象过点A（-1，6），
∴

m-8

-1

=6，解答m=2．
故m的值为2；
分别过点A、B作x轴的垂线，垂足分别为点E、D，
由题意得，AE=6，OE=1，
∵BD⊥x轴，AE⊥x轴，
∴AE∥BD，
∴△CBD∽△CAE，∴

CB

CA

=

BD

AE

，
∵AB=2BC，∴

CB

CA

=

1

3

，
∴

1

3

=

BD

6

，∴BD=2．
即点B的纵坐标为2．
∵B在反比例函数y=

-6

x

的图象上，
∴2=

-6

x

，
∴x=-3，
∵点A（-1，6），点B（-3，2）
∴直线AB的解析式为：y=2x+8，
∴C（-4，0）．
故选B．

点评：本题考查了一次函数和反比例函数的交点问题，将两函数联立求出交点是解决问题的关键，综合性较强，难度较大．