��Ŀ����
ʵ����̽��
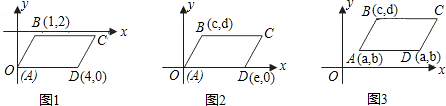
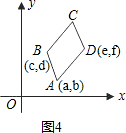
��1����ͼ1��ͼ2��ͼ3�У�����ƽ���ı���ABCD�Ķ���A��B��D�����꣬д��ͼ1��ͼ2��ͼ3�еĶ���C�����꣬���Ƿֱ���
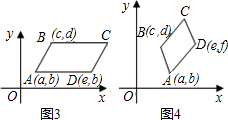
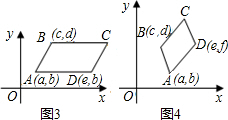
��2����ͼ4�У�����ƽ���ı���ABCD�Ķ���A��B��D�����꣨��ͼ��ʾ�����������C�����꣨C�������ú�a��b��c��d��e��f�Ĵ���ʽ��ʾ����
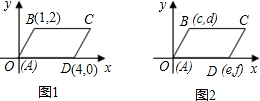
�����뷢��
��3��ͨ����ͼ1��ͼ2��ͼ3��ͼ4�Ĺ۲�Ͷ���C�������̽������ᷢ�֣�����ƽ���ı���ABCD����ֱ������ϵ���ĸ�λ�ã����䶥��C����Ϊ��m��n������ͼ4��ʱ�����ĸ�����ĺ�����a��c��m��e֮��ĵ�����ϵΪ
�������ƹ�
��4����ͬһֱ������ϵ����˫����y=-
��������G(-
c��
c)��S(
c��
c)��H��2c��0��������c��0�����ʵ�cΪ��ֵʱ����˫�����ϴ��ڵ�P��ʹ����G��S��H��PΪ������ı�����ƽ���ı��Σ���������з���������P�����꣮
��1����ͼ1��ͼ2��ͼ3�У�����ƽ���ı���ABCD�Ķ���A��B��D�����꣬д��ͼ1��ͼ2��ͼ3�еĶ���C�����꣬���Ƿֱ���
��5��2������e+c��d��
��5��2������e+c��d��
����e+c-a��d��
��e+c-a��d��
����2����ͼ4�У�����ƽ���ı���ABCD�Ķ���A��B��D�����꣨��ͼ��ʾ�����������C�����꣨C�������ú�a��b��c��d��e��f�Ĵ���ʽ��ʾ����
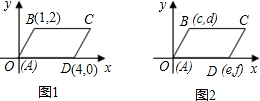

�����뷢��
��3��ͨ����ͼ1��ͼ2��ͼ3��ͼ4�Ĺ۲�Ͷ���C�������̽������ᷢ�֣�����ƽ���ı���ABCD����ֱ������ϵ���ĸ�λ�ã����䶥��C����Ϊ��m��n������ͼ4��ʱ�����ĸ�����ĺ�����a��c��m��e֮��ĵ�����ϵΪ
m=c+e-a
m=c+e-a
��������b��d��n��f֮��ĵ�����ϵΪn=d+f-b
n=d+f-b
������֤�������������ƹ�
��4����ͬһֱ������ϵ����˫����y=-
| 14 |
| x |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
��������1������ƽ���ı��ε����ʣ��Ա�ƽ������ȣ��ó�ͼ2��3�ж���C������ֱ��ǣ�e+c��d������c+e-a��d����
��2���ֱ����A��B��C��D��x��Ĵ��ߣ�����ֱ�ΪA1��B1��C1��D1���ֱ��A��D��AE��BB1��E��DF��CC1�ڵ�F����ƽ���ı���ABCD�У�CD=BA�������ڽǺͶ������֡�BB1��CC1�����Ƴ���EBA=��FCD����BEA�ա�CFD��������ó�AF=DF=a-c��BE=CF=d-b����C��x��y������e-x=a-c����x=e+c-a����y-f=d-b����y=f+d-b���̶��Ƴ���C�����꣮
��3����ƽ���ı���ABCD�У�CD=BA��ͬ��֤����BEA�ա�CFD��ͬ��2��֤������Ȼ���Ƴ�AF=DF=a-c��BE=CF=d-b������֪C�������Ϊ��m��n����e-m=a-c����m=e+c-a����n-f=d-b���ó�n=f+d-b��
��4����GSΪƽ���ı��εĶԽ��ߣ��ɣ�3���ɵ�P1��-2c��7c����ҪʹP1��˫�����ϣ�����-14c2=-14�����c��ʵ��ȡֵ�Լ�P1�����꣬��SHΪƽ���ı��εĶԽ��ߣ��ɣ�3���ɵ�P2��3c��2c����ͬ���ɵ�c=1����ʱP2��3��2������GHΪƽ���ı��εĶԽ��ߣ��ɣ�3���ɵã�c��-2c����ͬ���ɵ�c=1����ʱP3��1��-2���������������ɵý⣮
��2���ֱ����A��B��C��D��x��Ĵ��ߣ�����ֱ�ΪA1��B1��C1��D1���ֱ��A��D��AE��BB1��E��DF��CC1�ڵ�F����ƽ���ı���ABCD�У�CD=BA�������ڽǺͶ������֡�BB1��CC1�����Ƴ���EBA=��FCD����BEA�ա�CFD��������ó�AF=DF=a-c��BE=CF=d-b����C��x��y������e-x=a-c����x=e+c-a����y-f=d-b����y=f+d-b���̶��Ƴ���C�����꣮
��3����ƽ���ı���ABCD�У�CD=BA��ͬ��֤����BEA�ա�CFD��ͬ��2��֤������Ȼ���Ƴ�AF=DF=a-c��BE=CF=d-b������֪C�������Ϊ��m��n����e-m=a-c����m=e+c-a����n-f=d-b���ó�n=f+d-b��
��4����GSΪƽ���ı��εĶԽ��ߣ��ɣ�3���ɵ�P1��-2c��7c����ҪʹP1��˫�����ϣ�����-14c2=-14�����c��ʵ��ȡֵ�Լ�P1�����꣬��SHΪƽ���ı��εĶԽ��ߣ��ɣ�3���ɵ�P2��3c��2c����ͬ���ɵ�c=1����ʱP2��3��2������GHΪƽ���ı��εĶԽ��ߣ��ɣ�3���ɵã�c��-2c����ͬ���ɵ�c=1����ʱP3��1��-2���������������ɵý⣮
����⣺��1������ƽ���ı��ε����ʣ��Ա�ƽ������ȣ�
�ó�ͼ1��ͼ2��3�ж���C������ֱ��ǣ���5��2������e+c��d������c+e-a��d����
�ʴ�Ϊ����5��2������e+c��d������c+e-a��d����
��2���ֱ����A��B��C��D��x��Ĵ��ߣ�����ֱ�ΪA1��B1��C1��D1��
�ֱ��A��D��AE��BB1��E��DF��CC1�ڵ�F��
��ƽ���ı���ABCD�У�CD=BA��
�֡�BB1��CC1��
���EBA+��ABC+��BCF=��ABC+��BCF+��FCD=180�ȣ�
���EBA=��FCD��
�֡ߡ�BEA=��CFD=90�㣬
���BEA�ա�CFD��
��AE=DF=a-c��BE=CF=d-b��
��C��x��y����
��e-x=a-c����x=e+c-a��
��y-f=d-b����y=f+d-b��
��C��e+c-a��f+d-b����
�����ʽⷨ���֣��ɲ������֣�
��3��m=c+e-a��n=d+f-b��m+a=c+e��n+b=d+f��
��4����GSΪƽ���ı��εĶԽ��ߣ��ɣ�3���ɵ�P1��-2c��7c����
ҪʹP1��˫�����ϣ�
����-14c2=-14��
��c1=-1����������c��0����ȥ����c2=1����ʱP1��-2��7����
��SHΪƽ���ı��εĶԽ��ߣ��ɣ�3���ɵ�P2��3c��2c����
ͬ���ɵ�c=1����ʱP2��3��2������˫�����ϣ�
��GHΪƽ���ı��εĶԽ��ߣ��ɣ�3���ɵã�c��-2c����
ͬ���ɵ�c=1����ʱP3��1��-2������˫�����ϣ�
������������c=1ʱ��˫�����ϴ��ڵ�P��ʹ����G��S��H��PΪ������ı�����ƽ���ı��Σ�
���������ĵ���P1��-2��7����
�ó�ͼ1��ͼ2��3�ж���C������ֱ��ǣ���5��2������e+c��d������c+e-a��d����
�ʴ�Ϊ����5��2������e+c��d������c+e-a��d����
��2���ֱ����A��B��C��D��x��Ĵ��ߣ�����ֱ�ΪA1��B1��C1��D1��
�ֱ��A��D��AE��BB1��E��DF��CC1�ڵ�F��
��ƽ���ı���ABCD�У�CD=BA��
�֡�BB1��CC1��
���EBA+��ABC+��BCF=��ABC+��BCF+��FCD=180�ȣ�
���EBA=��FCD��
�֡ߡ�BEA=��CFD=90�㣬
���BEA�ա�CFD��
��AE=DF=a-c��BE=CF=d-b��
��C��x��y����

��e-x=a-c����x=e+c-a��
��y-f=d-b����y=f+d-b��
��C��e+c-a��f+d-b����
�����ʽⷨ���֣��ɲ������֣�
��3��m=c+e-a��n=d+f-b��m+a=c+e��n+b=d+f��
��4����GSΪƽ���ı��εĶԽ��ߣ��ɣ�3���ɵ�P1��-2c��7c����
ҪʹP1��˫�����ϣ�
����-14c2=-14��
��c1=-1����������c��0����ȥ����c2=1����ʱP1��-2��7����
��SHΪƽ���ı��εĶԽ��ߣ��ɣ�3���ɵ�P2��3c��2c����
ͬ���ɵ�c=1����ʱP2��3��2������˫�����ϣ�
��GHΪƽ���ı��εĶԽ��ߣ��ɣ�3���ɵã�c��-2c����
ͬ���ɵ�c=1����ʱP3��1��-2������˫�����ϣ�
������������c=1ʱ��˫�����ϴ��ڵ�P��ʹ����G��S��H��PΪ������ı�����ƽ���ı��Σ�
���������ĵ���P1��-2��7����
������������Ҫ������ƽ���ı��ε����ʣ�ƽ��ֱ������ϵ�ڵ����꣬ƽ���ߵ����ʵ�֪ʶ������ƽ���ı��ε��ص���ƽ��ֱ������ϵ�ǽ������Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
 ���Ķ����в��ϣ�
���Ķ����в��ϣ� ��ͼ����ƽ��ֱ������ϵ�У�����y=x��ͼ��l�ǵ�һ�������Ľ�ƽ���ߣ�
��ͼ����ƽ��ֱ������ϵ�У�����y=x��ͼ��l�ǵ�һ�������Ľ�ƽ���ߣ�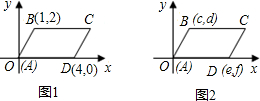
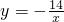 ��������
��������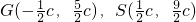 ��H��2c��0��������c��0�����ʵ�cΪ��ֵʱ����˫�����ϴ��ڵ�P��ʹ����G��S��H��PΪ������ı�����ƽ���ı��Σ���������з���������P�����꣮
��H��2c��0��������c��0�����ʵ�cΪ��ֵʱ����˫�����ϴ��ڵ�P��ʹ����G��S��H��PΪ������ı�����ƽ���ı��Σ���������з���������P�����꣮