题目内容
【题目】在每个小正方形的边长为 ![]() 的网格图形中,每个小正方形的顶点称为格点.从一个格点移动到与之相距
的网格图形中,每个小正方形的顶点称为格点.从一个格点移动到与之相距 ![]() 的另一个格点的运动称为一次跳马变换.例如,在
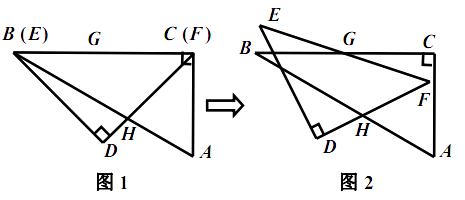
的另一个格点的运动称为一次跳马变换.例如,在 ![]() 的正方形网格图形中(如图1),从点
的正方形网格图形中(如图1),从点 ![]() 经过一次跳马变换可以到达点
经过一次跳马变换可以到达点 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 等处.现有
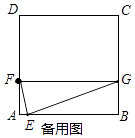
等处.现有 ![]() 的正方形网格图形(如图2),则从该正方形的顶点
的正方形网格图形(如图2),则从该正方形的顶点 ![]() 经过跳马变换到达与其相对的顶点
经过跳马变换到达与其相对的顶点 ![]() ,最少需要跳马变换的次数是( )
,最少需要跳马变换的次数是( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:由图一可知,沿AC或AD可进行下去,然后到CF,从而求出AF=3![]() ,此时可知跳过了3格,然后依次进行下去;而20×20的网格中共有21条线,所以要进行下去,正好是(20+1)÷3×2=14.
,此时可知跳过了3格,然后依次进行下去;而20×20的网格中共有21条线,所以要进行下去,正好是(20+1)÷3×2=14.
所以答案是B.
【考点精析】本题主要考查了勾股定理的概念的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.

练习册系列答案
相关题目