题目内容
 (2012•开封一模)如图,在Rt△ABC中,∠ABC=90°,斜边AC的垂直平分线交BC于点D,交AC于点E,连接BE.
(2012•开封一模)如图,在Rt△ABC中,∠ABC=90°,斜边AC的垂直平分线交BC于点D,交AC于点E,连接BE.(1)若BE是△DEC的外接圆的切线,求∠C的大小;
(2)当AB=1,AC=2时,求△DEC的外接圆的半径.
分析:(1)求出O在DC上,连接OE,得出∠EBO+∠BOE=90°,求出BE=EC=
AC,推出∠C=∠EBC,得出∠BOE=2∠C,即可求出∠C;
(2)求出EC,证△DEC∽△ABC,推出
=
,代入求出DC即可.
| 1 |
| 2 |
(2)求出EC,证△DEC∽△ABC,推出
| AC |
| DC |
| BC |
| EC |
解答:解:(1)∵DE垂直平分AC,
∴∠DEC=90°,
∴DC是⊙O的直径,
∴O在DC上,
连接OE,
∵BE是⊙O的切线,
∴∠OEB=90°,
∴∠EBO+∠BOE=90°,
在Rt△ABC中,E为斜边AC的中点,
∴BE=EC=AE=
AC(直角三角形斜边上中线等于斜边的一半),
∴∠EBO=∠C,
∵OC=OE,
∴∠C=∠CEO,
∵∠BOE=∠C+∠CEO,
∴∠BOE=2∠C,
∵∠EBO+∠BOE=90°,∠EBO=∠C
∴∠C+2∠C=90°,
∴∠C=30°;
(2)在Rt△ABC中,BC=
=
,
EC=
AC=1,
∵∠ABC=∠DEC=90°,∠C=∠C,
∴△DEC∽△ABC,
∴
=
,
∴
=
,
∴DC=
,
∴△DEC的外接圆的半径是
.

∴∠DEC=90°,
∴DC是⊙O的直径,
∴O在DC上,
连接OE,
∵BE是⊙O的切线,
∴∠OEB=90°,
∴∠EBO+∠BOE=90°,
在Rt△ABC中,E为斜边AC的中点,
∴BE=EC=AE=
| 1 |
| 2 |
∴∠EBO=∠C,
∵OC=OE,
∴∠C=∠CEO,
∵∠BOE=∠C+∠CEO,
∴∠BOE=2∠C,
∵∠EBO+∠BOE=90°,∠EBO=∠C
∴∠C+2∠C=90°,
∴∠C=30°;
(2)在Rt△ABC中,BC=
| AC2-AB2 |
| 3 |

EC=
| 1 |
| 2 |
∵∠ABC=∠DEC=90°,∠C=∠C,
∴△DEC∽△ABC,
∴
| AC |
| DC |
| BC |
| EC |
∴
| 2 |
| DC |
| ||
| 1 |
∴DC=
2
| ||
| 3 |
∴△DEC的外接圆的半径是
| ||
| 3 |
点评:本题考查的知识点是切线的性质、相似三角形的性质和判定、勾股定理、线段垂直平分线的性质,主要考查学生运用性质进行推理和计算的能力.

练习册系列答案
相关题目
 (2012•槐荫区一模)如图所示,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(-1,0)、(0,-3).
(2012•槐荫区一模)如图所示,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(-1,0)、(0,-3).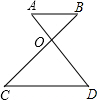 (2012•虹口区一模)如图,若AD=3AO,则当CO:BO的值为
(2012•虹口区一模)如图,若AD=3AO,则当CO:BO的值为 (2012•开封一模)将一副常规的三角板按如图方式放置,则图中∠AOB的度数为
(2012•开封一模)将一副常规的三角板按如图方式放置,则图中∠AOB的度数为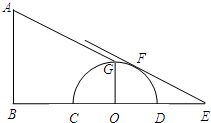 圆形广告牌的最高处G,而半圆形广告牌的影子刚好落在地面上一点E.已知BC=5米,DE=2米,半圆的直径CD=6米.
圆形广告牌的最高处G,而半圆形广告牌的影子刚好落在地面上一点E.已知BC=5米,DE=2米,半圆的直径CD=6米.