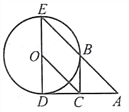
题目内容
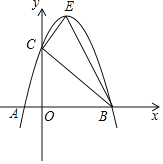
【题目】如图，已知抛物线
经过点
和点
，点C为抛物线与y轴的交点．
求抛物线的解析式；
若点E为直线BC上方抛物线上的一点，请求出
面积的最大值．
在条件下，是否存在这样的点
，使得
为等腰三角形？如果有，请直接写出点D的坐标；如果没有，请说明理由．
【答案】（1）
．（2）当
时，
面积取最大值，最大值为
．（3）点D的坐标为
、
、
、
或
【解析】分析：
根据点A、B的坐标利用待定系数法即可求出抛物线的解析式；
过点E作
轴，交BC于点F，利用二次函数图象上点的坐标特征可找出点C的坐标，根据点B、C的坐标利用待定系数法即可求出直线BC的解析式，设点E的坐标为
，则点F的坐标为
，进而可得出EF的长度，利用三角形的面积公式可得出
，配方后利用二次函数的性质即可求出面积的最大值；
分
、
、
三种情况考虑，根据等腰三角形的性质结合两点间的距离公式，即可得出关于m的一元二次
或一元一次
方程，解之即可得出结论．
详解：将
、
代入
，
得：
，解得：
，
抛物线的解析式为．
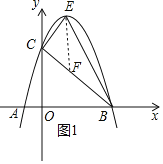
过点E作轴，交BC于点F，如图1所示．
当
时，
，
点C的坐标为
．
设直线BC的解析式为
，
将、
代入，得：
，解得：
，
直线BC的解析式为
．
设点E的坐标为，则点F的坐标为，
，
，
当时，面积取最大值，最大值为．
由可知点E的坐标为
为等腰三角形分三种情况如图
：
当时，有
，
解得：
，
，
点D的坐标为或；
当时，有
，
解得：
，
点D的坐标为；
当时，有
，
解得：
，
，
点D的坐标为或
综上所述：当点D的坐标为、、、或时，为等腰三角形．
练习册系列答案
阅读快车系列答案
相关题目
