题目内容
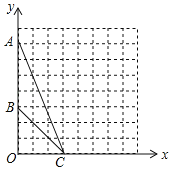
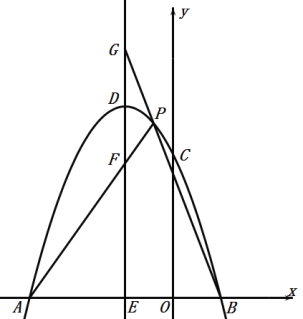
【题目】如图,在平面直角坐标系中,抛物线![]() 交
交![]() 轴
轴![]() 、
、![]() 两点(
两点(![]() 在
在![]() 的左侧),且
的左侧),且![]() ,
,![]() ,与
,与![]() 轴交于
轴交于![]() ,抛物线的顶点坐标为
,抛物线的顶点坐标为![]() .
.
(1)求![]() 、
、![]() 两点的坐标;
两点的坐标;
(2)求抛物线的解析式;
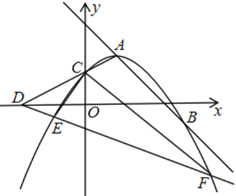
(3)过点![]() 作直线
作直线![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,点
,点![]() 是抛物线上
是抛物线上![]() 、
、![]() 两点间的一个动点(点
两点间的一个动点(点![]() 不与
不与![]() 、
、![]() 两点重合),
两点重合),![]() 、
、![]() 与直线
与直线![]() 分别交于点
分别交于点![]() 、
、![]() ,当点
,当点![]() 运动时,
运动时,![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
【答案】(1)![]() 点坐标
点坐标![]() ,
,![]() 点坐标
点坐标![]() ;(2)
;(2)![]() ;(3)是定值,定值为8
;(3)是定值,定值为8
【解析】
(1)由OA、OB的长可得A、B两点坐标;
(2)结合题意可设抛物线的解析式为![]() ,将点C坐标代入求解即可;
,将点C坐标代入求解即可;
(3)过点![]() 作
作![]() 轴交
轴交![]() 轴于
轴于![]() ,设
,设![]() ,可用含t的代数式表示出
,可用含t的代数式表示出![]() ,
,![]() ,
,![]() 的长,利用
的长,利用![]() ,
,![]() 的性质可得EF、EG的长,相加可得结论.
的性质可得EF、EG的长,相加可得结论.
(1)由抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 的左侧),且
的左侧),且![]() ,
,
![]() ,得
,得
![]() 点坐标
点坐标![]() ,
,![]() 点坐标
点坐标![]() ;
;
(2)设抛物线的解析式为![]() ,
,
把![]() 点坐标代入函数解析式,得
点坐标代入函数解析式,得
![]() ,
,
解得![]() ,
,
抛物线的解析式为
![]() ;
;
(3)![]() (或
(或![]() 是定值),理由如下:
是定值),理由如下:
过点![]() 作
作![]() 轴交
轴交![]() 轴于
轴于![]() ,如图
,如图
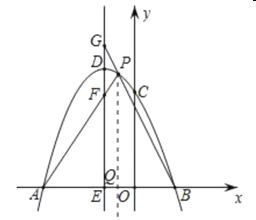
设![]() ,
,
则![]() ,
,![]() ,
,
![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴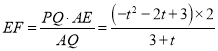
![]()
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴
![]()
∴![]()

练习册系列答案
相关题目