题目内容
在直角梯形ABCD中,AB∥DC,AB⊥BC,∠A=60°,AB=2CD,E、F分别为AB、AD的中点,连结EF、EC、BF、CF。。
⑴判断四边形AECD的形状(不证明);
⑵在不添加其它条件下,写出图中一对全等的三角形,用符号“≌”表示,并证明。
⑶若CD=2,求四边形BCFE的面积。

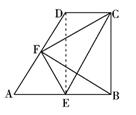
(1)平行四边形
(2)△BEF≌△FDC或(△AFB≌△EBC≌△EFC)
证明:连结DE ∵AB=2CD,E为AB中点 ∴DC=EB 又∵ DC∥EB 四边形BCDE是平行四边形
∵AB⊥BC ∴四边形BCDE为矩形 ∴∠AED=90° Rt△ABE中,∠A=60°,F为AD中点
∴AE=![]() AD=AF=FD ∴△AEF为等边三角形 ∴∠BEF=180°-60°=120° 而∠FDC=120°
AD=AF=FD ∴△AEF为等边三角形 ∴∠BEF=180°-60°=120° 而∠FDC=120°
得△BEF≌△FDC(S.A.S.)
(3)若CD=2,则AD=4,DE=BC=2![]() ∵S△ECF=
∵S△ECF=![]() SAECD=
SAECD=![]() CD?DE=
CD?DE=![]() ×2×2
×2×2![]() =2
=2![]()
S△CBE=![]() BE?BC=
BE?BC=![]() ×2×2
×2×2![]() =2
=2![]() ∴S四边形BCFE=S△ECF+S△EBC=2
∴S四边形BCFE=S△ECF+S△EBC=2![]() +2
+2![]() =4
=4![]()

练习册系列答案
相关题目
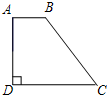 如图,在直角梯形ABCD中,AB∥DC,∠D=90°,若AD=8,BC=10,则cosC的值为( )
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,若AD=8,BC=10,则cosC的值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
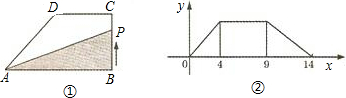
 如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,且AB=BC=4AD,E是AB上的一点,DE⊥EC.求证:CE平分∠BCD.
如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,且AB=BC=4AD,E是AB上的一点,DE⊥EC.求证:CE平分∠BCD. 如图,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿过点D的直线折叠,使点A刚好落在BC边上,则此时折痕的长为
如图,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿过点D的直线折叠,使点A刚好落在BC边上,则此时折痕的长为 如图,在直角梯形ABCD中,若AD=5,点A的坐标为(-2,7),则点D的坐标为( )
如图,在直角梯形ABCD中,若AD=5,点A的坐标为(-2,7),则点D的坐标为( )