题目内容
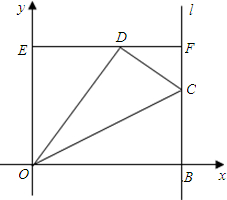
如图，
，D、E分别是半径OA和OB的中点，CD与CE的大小有什么关系？为什么？
【答案】分析：应该是相等的关系，可通过构建全等三角形来实现，连接OC，只要证明三角形OCD和OEC全等即可．有了一条公共边，根据圆心角定理我们可得出∠AOB=∠BOC，又有OD=OE（同为半径的一半），这样就构成了SAS的条件．因此便可得出两三角形全等．
解答：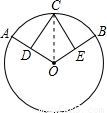
解：CD=CE．
理由是：连接OC，
∵D、E分别是OA、OB的中点，
∴OD=OE，
又∵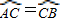
，∴∠DOC=∠EOC，
OC=OC，∴△CDO≌△CEO，
∴CD=CE．
点评：此题考查简单的线段相等，可以通过作辅助线构建全等三角形来证明．
解答：
解：CD=CE．理由是：连接OC，
∵D、E分别是OA、OB的中点，
∴OD=OE，
又∵
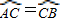，∴∠DOC=∠EOC，OC=OC，∴△CDO≌△CEO，
∴CD=CE．
点评：此题考查简单的线段相等，可以通过作辅助线构建全等三角形来证明．
练习册系列答案
相关题目
甲、乙分别从A地、B地同时相向而行．他们离开A地的路程y（km/h） 和行走的时间x（h）之间的函数关系如图所示，解析式分别是y1=4x和y2=-3x+6．
，S△DOH：S△DHC=1：4，求G点坐标．
