题目内容
如图，在⊙O中，∠AOB=120°，AB=3，则圆心O到边AB的距离=分析：过O作OC⊥AB，根据垂径定理，∠AOC=60°，AC=
AB．再根据∠AOC的正切即可求出OC．
| 1 |
| 2 |
解答：
解：过O作OC⊥AB，垂足为C．
∵∠AOB=120°，AB=3，
∴∠AOC=60°，AC=
AB=
．
∴tan∠AOC=
=
，
OC=
×
=
．
解：过O作OC⊥AB，垂足为C．∵∠AOB=120°，AB=3，
∴∠AOC=60°，AC=
| 1 |
| 2 |
| 3 |
| 2 |
∴tan∠AOC=
| AC |
| OC |
| 3 |
OC=
| 3 |
| 2 |
| ||
| 3 |
| ||
| 2 |
点评：本题利用垂径定理构造出直角三角形，再根据角的正切函数求解．
练习册系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
相关题目
19、如图，在△ABC中，CD⊥AB于D，FG⊥AB于G，ED∥BC，试说明∠1=∠2，以下是证明过程，请填空：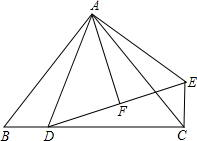
如图，在△ABC中，已知AB=AC，∠BAC=90°，D是BC上一点，EC⊥BC，EC=BD，DF=FE．求证：
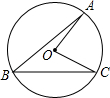如图，在⊙O中，∠ABC=40°，则∠AOC=
如图，在△ABC中，∠B，∠C的外角平分线相交于点O，若∠A=74°，则∠O=
15、如图，在△ABC中，AQ=PQ，PR=PS，PS⊥AC于S，PR⊥AB于R，则以下结论中：（1）AS=AR；（2）△BRP∽△QSP；（3）PQ∥AB中，正确的有