题目内容
【题目】已知，抛物线y=ax2﹣
ax﹣4a与x轴交于A，B两点，与y轴交于C点，A点在B点左侧，C点在x轴下方，且△AOC∽△COB
（1）求这条抛物线的解析式及直线BC的解析式；
（2）设点D为抛物线对称轴上的一点，当点D在对称轴上运动时，是否可以与点C，A，B三点，构成梯形的四个顶点？若可以，求出点D坐标，若不可以，请说明理由．
【答案】（1）y=
x2﹣
x﹣2，y=x﹣2；（2）见解析
【解析】分析：（1）将函数解析式变形为y=a（x-2
）（x+）可得A、B坐标，由解析式知C（0，-4a），根据△AOC∽△COB知
，据此求得a的值，进一步可得抛物线和直线BC解析式；
（2）分CD1∥AB、AD2∥BC、BD3∥AC三种情况，利用相似三角形的性质分别求解可得答案．
详解：（1）∵y=ax2﹣x﹣4a=a（x﹣2）（x+），
∴由a（x﹣2）（x+）=0且a≠0可得x=2或x=，
由题意知点A（﹣，0）、B（2，0），
当x=0时，y=﹣4a，
∴点C（0，﹣4a），
∵C点在x轴下方，
∴﹣4a＜0，a＞0，
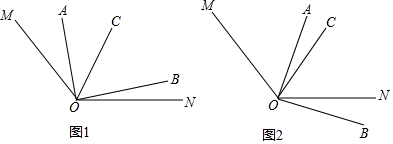
如图1所示，
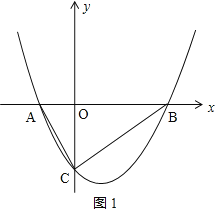
∵△AOC∽△COB，
∴，即
，
解得：a=﹣（舍）或a=，
则抛物线解析式为y=x2﹣x﹣2，点C坐标为（0，﹣2），
设直线BC解析式为y=kx+b，
将B（2，0）、C（0，﹣2）代入，得：
，
解得：
，
∴直线BC解析式为y=x﹣2；
（2）抛物线的对称轴为x=
，
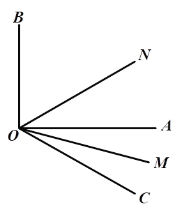
①如图2，当CD1∥AB时，四边形ACD1B为梯形，
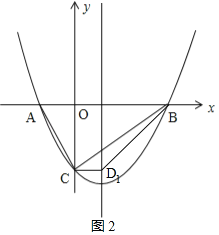
∵点C（0，﹣2），
∴点D1坐标为（，﹣2）；
②如图3，当AD2∥BC时，四边形ACBD2为梯形，
∴∠D2AE=∠CBO，
∵∠AED2=∠BOC=90°，
∴△AD2E∽△BOC，
∴
，即
，
解得：D2E=
，
∴点D2坐标为（，）；
③如图4，当BD3∥AC时，四边形ACBD3为梯形，
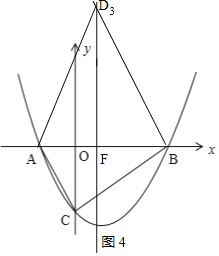
∴∠OAC=∠FBD3，
∵∠AOC=∠BFD3=90°，
∴△AOC∽△BFD3，
∴
，即
，
解得：FD3=3，
∴点D3的坐标为（，3）；
综上，点D的坐标为（，﹣2）或（，）或（，3）．
