题目内容
如图,函数y=| k | x |
 作y轴的垂线,垂足为C,连接AB,AC.
作y轴的垂线,垂足为C,连接AB,AC.(1)求k的值;
(2)若△ABC的面积为4,求点B的坐标.
分析:(1)根据反比例函数上的点的坐标,横纵坐标的乘积相等,等于k求解即可;
(2)根据反比例函数上点的特点可求得ab=4,再根据△ABC的面积为4求得a,b之间的另一个关系式,代入ab值即可求得a值,从而求出b值,得到点B的坐标.
(2)根据反比例函数上点的特点可求得ab=4,再根据△ABC的面积为4求得a,b之间的另一个关系式,代入ab值即可求得a值,从而求出b值,得到点B的坐标.
解答:解:(1)∵函数y=
(x>0,k是常数)的图象经过A(1,4)
∴k=1×4=4.
(2)由(1)可知y=
,
∴ab=4
∵BC=a,OC=b
∴
a(4-b)=4
即4a-ab=8
∴a=3,b=
即点B的坐标为(3,
).
| k |
| x |
∴k=1×4=4.
(2)由(1)可知y=
| 4 |
| x |
∴ab=4
∵BC=a,OC=b
∴
| 1 |
| 2 |
即4a-ab=8
∴a=3,b=
| 4 |
| 3 |
即点B的坐标为(3,
| 4 |
| 3 |
点评:此题综合考查了反比例函数的性质,综合性比较强,注意反比例函数上的点向x轴y轴引垂线形成的矩形面积(反比例函数上的点的坐标,横纵坐标的乘积相等)等于反比例函数的k值.

练习册系列答案
相关题目
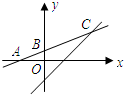 如图,函数y=kx+b的图象与x轴,y轴分别交于A(-2,0),B(0,1)两点,那么此函数的图象与函数y=x-1的图象交点C的坐标是
如图,函数y=kx+b的图象与x轴,y轴分别交于A(-2,0),B(0,1)两点,那么此函数的图象与函数y=x-1的图象交点C的坐标是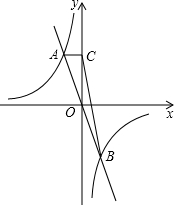 如图,函数y=-kx与
如图,函数y=-kx与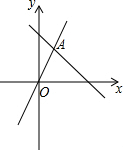 (2013•鄞州区模拟)如图,函数y=kx和y=-
(2013•鄞州区模拟)如图,函数y=kx和y=- 如图,函数y=
如图,函数y=