题目内容
已知:正方形ABCD的边长为3,点P是直线CD上一点,若DP=1,则tan∠BPC的值是________.
 或
或
分析:分类讨论:当点P在边DC上,根据正方形的性质有BC=DC=3,而DP=1,则PC=3-1=2,根据正切的定义得到tan∠BPC=
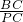 =
= ;当点P在边CD的延长线上,此时PC=PD+DC=1+3=4,根据正切的定义得到tan∠BPC=
;当点P在边CD的延长线上,此时PC=PD+DC=1+3=4,根据正切的定义得到tan∠BPC=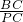 =
= .
.解答:当点P在边DC上,如图1,
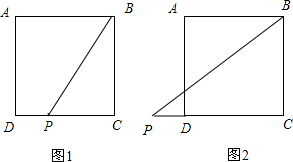
∵四边形ABCD为边长为3的正方形,
∴BC=DC=3,
而DP=1,
∴PC=3-1=2,
∴tan∠BPC=
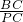 =
= ;
;当点P在边CD的延长线上,如图2,
则PC=PD+DC=1+3=4,
∴tan∠BPC=
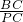 =
= .
.故答案为
 或
或 .
.点评:本题考查了正切的定义:在直角三角形中,一个锐角的正切等于这个角的对边与邻边的比值.也考查了正方形的性质以及分类讨论思想的运用.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
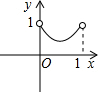
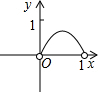
 如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是( )
如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是( )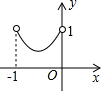
 由.
由. s的速度运动,同时动点Q在线段FC上从F?C以1cm/s的速度运动,动点G在PC上,且∠EGC=∠EQC,连接PD.设运动时间为t秒.
s的速度运动,同时动点Q在线段FC上从F?C以1cm/s的速度运动,动点G在PC上,且∠EGC=∠EQC,连接PD.设运动时间为t秒. 18、如图,已知在正方形ABCD中,P是BC上的一点,且AP=DP.求证:P是BC中点.
18、如图,已知在正方形ABCD中,P是BC上的一点,且AP=DP.求证:P是BC中点. 如图,已知在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=
如图,已知在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=