题目内容
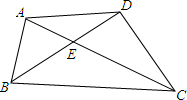 已知:如图,四边形ABCD中,对角线AC、BD相交于点E,BD⊥DC,∠ABD=45°,∠ACD=30°,AD=CD=2
已知:如图,四边形ABCD中,对角线AC、BD相交于点E,BD⊥DC,∠ABD=45°,∠ACD=30°,AD=CD=2 ,求AC和BD的长.
,求AC和BD的长.
解:∵BD⊥DC,
∴∠BDC=90°,
∵∠ACD=30°,AD=CD=2 ,
,
∴∠DEC=60°,∠DAC=∠ACD=30°,
DE=CD•tan30°=2 ×
× =2,
=2,
∴EC=2DE=4,∠ADE=30°,
∴AE=DE=2,
∴AC=AE+EC=2+4=6,
过点A作AM⊥BD,垂足为M,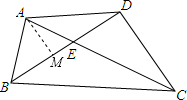
∵∠AEB=∠DEC=60°,
∴AM=AE•sin60°=2× =
= ,
,
ME=AEcos60°=2× =1,
=1,
∵∠ABD=45°,
∴BM=AM= ,
,
∴BBM+ME+DE= +1+2=3+
+1+2=3+ .
.
分析:通过解直角三角形求出DE长,求出EVC,即可求出AC,过点A作AM⊥BD,垂足为M,求出AM,ME,即可求出BD.
点评:本题考查了三角形的内角和定理,等腰三角形的性质,三角形的外角性质,解直角三角形的应用,主要考查学生的计算能力.
∴∠BDC=90°,
∵∠ACD=30°,AD=CD=2
 ,
,∴∠DEC=60°,∠DAC=∠ACD=30°,
DE=CD•tan30°=2
 ×
× =2,
=2,∴EC=2DE=4,∠ADE=30°,
∴AE=DE=2,
∴AC=AE+EC=2+4=6,
过点A作AM⊥BD,垂足为M,

∵∠AEB=∠DEC=60°,
∴AM=AE•sin60°=2×
 =
= ,
,ME=AEcos60°=2×
 =1,
=1,∵∠ABD=45°,
∴BM=AM=
 ,
,∴BBM+ME+DE=
 +1+2=3+
+1+2=3+ .
.分析:通过解直角三角形求出DE长,求出EVC,即可求出AC,过点A作AM⊥BD,垂足为M,求出AM,ME,即可求出BD.
点评:本题考查了三角形的内角和定理,等腰三角形的性质,三角形的外角性质,解直角三角形的应用,主要考查学生的计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
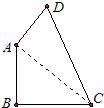 已知,如图,四边形ABCD中∠B=90°,AB=9,BC=12,AD=8,CD=17.
已知,如图,四边形ABCD中∠B=90°,AB=9,BC=12,AD=8,CD=17.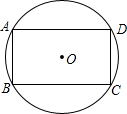 已知:如图,四边形ABCD内接于⊙O,且AB∥CD,AD∥BC,
已知:如图,四边形ABCD内接于⊙O,且AB∥CD,AD∥BC, 已知,如图,四边形ABCD是正方形,E、F分别是AB和AD延长线上的点,且BE=DF
已知,如图,四边形ABCD是正方形,E、F分别是AB和AD延长线上的点,且BE=DF 已知:如图,四边形ABCD中,BC=CD=10,AB=15,AB⊥BC,CD⊥BC,若把四边形ABCD绕直线AB旋转一周,则所得几何体的表面积是多少?
已知:如图,四边形ABCD中,BC=CD=10,AB=15,AB⊥BC,CD⊥BC,若把四边形ABCD绕直线AB旋转一周,则所得几何体的表面积是多少? 已知:如图,四边形ABCD及一点P.
已知:如图,四边形ABCD及一点P.