题目内容
如图,桌面内,直线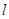 上摆放着两块大小相同的直角三角板,它们中较大锐角的度数为
上摆放着两块大小相同的直角三角板,它们中较大锐角的度数为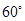 .将
.将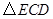 沿直线
沿直线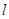 向左平移到图的位置,使E点落在AB上,即点
向左平移到图的位置,使E点落在AB上,即点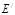 ,点P为AC与
,点P为AC与 的交点.
的交点.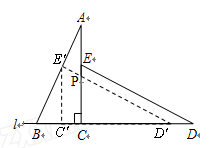
(1)求∠CPD'的度数;
(2)求证:AB⊥
 .
.
60°,解析:
根据直角三角板的角的特点求。
(1)在直角三角形C'E'D'中,
∠C'D' E'=180°–∠E' C'D'–∠C'E'D'
=180°–90°–60°=30°.
在直角三角形CPD'中,
∠CPD'=180°–∠P CD'–∠CD'P
=180°–90°–30 °=60°.
(2)∵∠A'E'D'=∠CPD'+∠E'BD'
=30°+60°=90°,
∴AB⊥ .
.
根据直角三角板的角的特点求。
(1)在直角三角形C'E'D'中,
∠C'D' E'=180°–∠E' C'D'–∠C'E'D'
=180°–90°–60°=30°.
在直角三角形CPD'中,
∠CPD'=180°–∠P CD'–∠CD'P
=180°–90°–30 °=60°.
(2)∵∠A'E'D'=∠CPD'+∠E'BD'
=30°+60°=90°,
∴AB⊥
 .
. 
练习册系列答案
相关题目

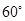 .将
.将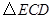 沿直线
沿直线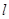 向左平移到图的位置,使E点落在AB上,即点
向左平移到图的位置,使E点落在AB上,即点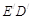 的交点.
的交点.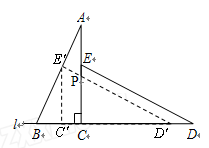
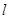 上摆放着两块大小相同的直角三角板,它们中较大锐角的度数为
上摆放着两块大小相同的直角三角板,它们中较大锐角的度数为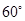 .将
.将 沿直线
沿直线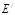 ,点P为AC与
,点P为AC与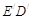 的交点.
的交点.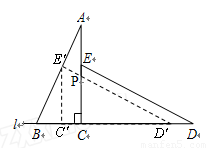
 上摆放着两块大小相同的直角三角板,它们中较大锐角的度数为
上摆放着两块大小相同的直角三角板,它们中较大锐角的度数为 .将
.将 沿直线
沿直线 ,点P为AC与
,点P为AC与 的交点.
的交点.