题目内容
抛物线y=ax2+bx+c经过直角△ABC的顶点A(-1,0),B(4,0),直角顶点C在y轴上,若抛物线的顶点在△ABC的内部(不包括边界),则a的范围是________.
- <a<0或0<a<
<a<0或0<a<
分析:根据点A、B的坐标求出OA、OB的长,再求出△ACO和△CBO相似,根据相似三角形对应边成比例列式求出OC的长,再根据二次函数的对称性求出对称轴,设对称轴与直线BC相交于P,与x轴交于Q,利用∠ABC的正切值求出点P到x轴的距离PQ,设抛物线的交点式解析式y=a(x+1)(x-4),整理求出顶点坐标,再根据抛物线的顶点在△ABC的内部分两种情况列式求出a的取值范围即可.
解答: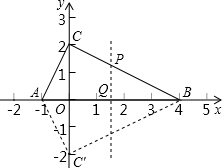 解:∵点A(-1,0),B(4,0),
解:∵点A(-1,0),B(4,0),
∴OA=1,OB=4,
易得△ACO∽△CBO,
∴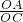 =
= ,
,
即 =
=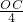 ,
,
解得OC=2,
∵抛物线y=ax2+bx+c经过A(-1,0),B(4,0),
∴对称轴为直线x=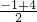 =
= ,
,
设对称轴与直线BC相交于P,与x轴交于Q,
则BQ=4- =2.5,
=2.5,
tan∠ABC= =
=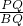 ,
,
即 =
=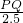 ,
,
解得PQ= ,
,
设抛物线的解析式为y=a(x+1)(x-4),
则y=a(x2-3x-4)=a(x- )2-
)2- a,
a,
当点C在y轴正半轴时,0<- a<
a< ,
,
解得- <a<0,
<a<0,
当点C在y轴负半轴时,- <-
<- a<0,
a<0,
解得0<a< ,
,
所以,a的取值范围是- <a<0或0<a<
<a<0或0<a< .
.
故答案为:- <a<0或0<a<
<a<0或0<a< .
.
点评:本题考查了二次函数的性质,相似三角形的判定与性质,把二次函数的解析式用交点式形式表示更加简便,注意要分点C在y正半轴和负半轴两种情况讨论.
 <a<0或0<a<
<a<0或0<a<
分析:根据点A、B的坐标求出OA、OB的长,再求出△ACO和△CBO相似,根据相似三角形对应边成比例列式求出OC的长,再根据二次函数的对称性求出对称轴,设对称轴与直线BC相交于P,与x轴交于Q,利用∠ABC的正切值求出点P到x轴的距离PQ,设抛物线的交点式解析式y=a(x+1)(x-4),整理求出顶点坐标,再根据抛物线的顶点在△ABC的内部分两种情况列式求出a的取值范围即可.
解答:
 解:∵点A(-1,0),B(4,0),
解:∵点A(-1,0),B(4,0),∴OA=1,OB=4,
易得△ACO∽△CBO,
∴
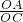 =
= ,
,即
 =
=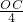 ,
,解得OC=2,
∵抛物线y=ax2+bx+c经过A(-1,0),B(4,0),
∴对称轴为直线x=
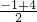 =
= ,
,设对称轴与直线BC相交于P,与x轴交于Q,
则BQ=4-
 =2.5,
=2.5,tan∠ABC=
 =
=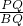 ,
,即
 =
=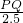 ,
,解得PQ=
 ,
,设抛物线的解析式为y=a(x+1)(x-4),
则y=a(x2-3x-4)=a(x-
 )2-
)2- a,
a,当点C在y轴正半轴时,0<-
 a<
a< ,
,解得-
 <a<0,
<a<0,当点C在y轴负半轴时,-
 <-
<- a<0,
a<0,解得0<a<
 ,
,所以,a的取值范围是-
 <a<0或0<a<
<a<0或0<a< .
.故答案为:-
 <a<0或0<a<
<a<0或0<a< .
.点评:本题考查了二次函数的性质,相似三角形的判定与性质,把二次函数的解析式用交点式形式表示更加简便,注意要分点C在y正半轴和负半轴两种情况讨论.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
已知点(2,8)在抛物线y=ax2上,则a的值为( )
| A、±2 | ||
B、±2
| ||
| C、2 | ||
| D、-2 |
若(2,0)、(4,0)是抛物线y=ax2+bx+c上的两个点,则它的对称轴是直线( )
| A、x=0 | B、x=1 | C、x=2 | D、x=3 |


 (2012•陕西)如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
(2012•陕西)如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.