题目内容
如图：A、B两点与建筑物底部D在一直线上，从建筑物顶部C点测得A、B两点的俯角分别是30°、60°，且AB=20，求建筑物CD的高．
解：由题意可知∠ECA=30°，∠ECB=60°，
∴∠BAC=30°，∠ECA=∠CAB=30°，
∴∠BCA=BAC=30°，
∴AB=BC=20，
∵∠BDC=30°，
∴BD=10，
∴DC=
=10
，
答：建筑物CD的高是10．
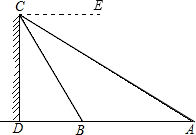
分析：由题意可知∠ECA=30°，∠ECB=60°，所以可证明△ABC是等腰三角形，所以AB=BC，解直角三角形BDC，进而求出建筑物CD的高．
点评：本题考查了勾股定理的应用和解直角三角形的应用，本题要求学生借助仰角关系构造直角三角形，并结合图形利用三角函数解直角三角形．
∴∠BAC=30°，∠ECA=∠CAB=30°，
∴∠BCA=BAC=30°，
∴AB=BC=20，
∵∠BDC=30°，
∴BD=10，
∴DC=
=10，答：建筑物CD的高是10
．分析：由题意可知∠ECA=30°，∠ECB=60°，所以可证明△ABC是等腰三角形，所以AB=BC，解直角三角形BDC，进而求出建筑物CD的高．
点评：本题考查了勾股定理的应用和解直角三角形的应用，本题要求学生借助仰角关系构造直角三角形，并结合图形利用三角函数解直角三角形．
练习册系列答案
相关题目
15km，CB=10km，现在要在铁路AB上建一个土特产品收购站E，使得C，D两村到E站的距离相等．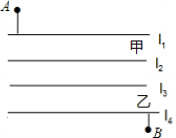
如图，五羊大学建立分校，校本部与分校隔着两条平行的小河，l1∥l2表示小河甲，l3∥l4表示小河乙，A为校本部大门，B为分校大门，为方便人员来往，要在两条小河上各建一座桥，桥面垂直于河岸．图中的尺寸是：甲河宽8米，乙河宽10米，A到甲河垂直距离为40米，B到乙河垂直距离为20米，两河距离100米，A、B两点水平距离（与小河平行方向）120米，为使A、B两点间来往路程最短，两座桥都按这个目标而建，那么，此时A、D两点间来往的路程是多少米？
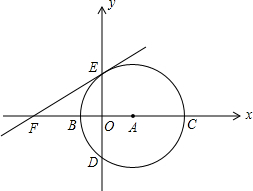于B、C两点，与y轴相交于D、E两点．
（2013•建邺区一模）如图，在直角坐标系中，直线y=2x与双曲线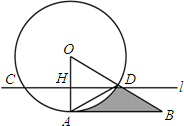
（2013•建邺区一模）如图，直线l与⊙O交于C、D两点，且与半径OA垂直，垂足为H，∠ODC=30°，在OD的延长线上取一点B，使得AD=BD．