Question

已知一次函数y＝mx＋4具有性质：y随x的增大而减小，又直线y＝mx＋4分别与直线x＝1与x＝4相交于点A、D，且点A在第一象限内，直线x＝1，x＝4分别与x轴相交于点B、C．

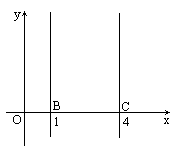
(1)要使四边形ABCD为凸四边形，求m的取值范围．

(2)已知四边形ABCD为凸四边形，直线y＝mx＋4与x轴相交于点E，当＝时，求这个一次函数的解析式．

(3)在(2)条件下，设直线y＝mx＋4与y轴相交于点F，求证：D为EF的中点．

Answer 1

答案：
解析：

(1)m的取值范围－1＜m＜0． 　　(2)∵四边形ABCD为凸四边形．∴m＋4＞0，4m＋4＞0，AB＝m＋4，DC＝4m＋4，∵AB⊥OX，DC⊥OX．∴AB∥CD．∴，又；∴．得m＝－．∴一次函数的解析式为：y＝－x＋4． 　　(3)由(2)中y＝－x＋4．可得此直线与x轴，y轴的交点坐标为E(8，0)、F(0，4)，∴点C(4，0)．∴OC＝EC，∴点C是线段OE的中点，又在Rt△EOF中，∵DC∥OF．∴D为FE的中点