题目内容
【题目】在
中，
，
，
为
边的中点，
，
绕点旋转，它的两边分别交
和
（或它们的延长线）于
，
.
（1）当
于时（如图1），可得
______________
.
（2）当
与不垂直时（如图2），第（1）小题得到的结论成立吗？若成立，请给予证明；若不成立，请直接给出
，
，的关系.
（3）当点在延长线上时（如图3），第（1）小题得到的结论成立吗？若成立，请给予证明；若不成立，请直接给出，，的关系.
【答案】（1）
；（2）成立，理由详见解析；（3）
【解析】
（1）当∠EDF绕D点旋转到DE⊥AC时，四边形CEDF是正方形，边长是AC的一半，即可得出结论；
（2）成立；先证明△CDE≌△BDF，即可得出结论；
（3）不成立；同（2）得：△DEC≌△DBF，得出
解:（1）当∠EDF绕D点旋转到DE⊥AC时，四边形CEDF是正方形；设△ABC的边长AC=8C=a，则正方形CEDF的边长为号a，
∴
，正方形CEDP的面积
；
∴
,故答案为：；
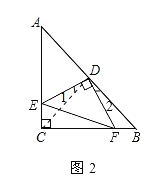
（2）成立.
证明：连接
，∵
（已知）
∴
（等边对等角）
∵
（已知），
（三角形内角和为180度）
∴
（等式性质）
∵（已知），
（中点的意义）
∴
（等腰三角形的三线合一）
∴
（垂直的意义）
∵
（三角形内角和为180度）
∴
(等式性质)
∴
（等量代换）
∴
（等角对等边）
∵（已证）
∴
（垂直的意义）
∵
（已知）
∴
（等式性质）
在
与
中，
∴
∴
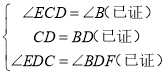
（全等三角形的面积相等）
∴
（等量代换）
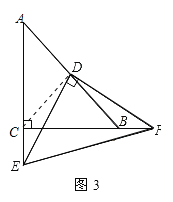
（3）不成立；；理由如下：连接CD，如图3所示：
同（2）得：
∴
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
