题目内容
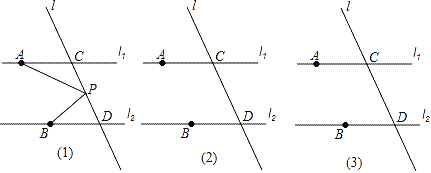
【题目】如图,已知直线l1∥l2,直线l和直线l1、l2交于点C和D,在C、D之间有一点P,A是l1上的一点,B是l2上的一点.
(1)如果P点在C、D之间运动时,如图(1)问∠PAC,∠APB,∠PBD之间有何关系,并说明理由.
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),在图(2),图(3)中画出图形并探索∠PAC,∠APB,∠PBD之间的关系又是如何?并选择其中一种情况说明理由.
【答案】(1)∠APB=∠PAC+∠PBD;
(2)当点P在C、D两点的外侧运动,且在l2下方时,∠PAC=∠PBD+∠APB.当点P在C、D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB.理由见解析.
【解析】
(1)当P点在C、D之间运动时,首先过点P作PE∥l1,由l1∥l2,可得PE∥l2∥l1,根据两直线平行,内错角相等,即可求得:∠APB=∠PAC+∠PBD;
(2)当点P在C、D两点的外侧运动时,由直线l1∥l2,根据两直线平行,同位角相等与三角形外角的性质,即可求得:∠PBD=∠PAC+∠APB.
解:(1)如图1,当P点在C、D之间运动时,∠APB=∠PAC+∠PBD.

理由如下:过点P作PE∥l1,
∵l1∥l2
∴PE∥l2∥l1,
∴∠PAC=∠1,∠PBD=∠2,
∴∠APB=∠1+∠2=∠PAC+∠PBD;
(2)如图2,当点P在C、D两点的外侧运动,且在l2下方时,∠PAC=∠PBD+∠APB.
理由如下:∵PE∥l2∥l1,
∴∠EPA=∠PAC,
∵∠EPA=∠PBD+∠APB,
∴∠PAC=∠PBD+∠APB.
如图3,当点P在C、D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB.
理由如下:∵PE∥l2∥l1,
∴∠EPB=∠PBD,
∵∠EPB=∠PAC+∠APB,
∴∠PBD=∠PAC+∠APB.

 阅读快车系列答案
阅读快车系列答案