题目内容
梯形ABCD中，AD∥BC，AD=2cm，BC=5cm，则S△ADC：S△ABC等于
- A.2：5
- B.3：5
- C.4：5
- D.1：5
A
分析：△ADC和△ABC的高相等，即比较两三角形的底边长即可．
解答：设△ADC和△ABC的高为h，
S△ADC=
×AD×h，S△ABC=×BC×h，
又AD=2cm，BC=5cm，
S△ADC：S△ABC=AD：BC=2：5．
故选A．
点评：本题考查了梯形的知识，难度不大，观察出△ADC和△ABC的高相等是关键．
分析：△ADC和△ABC的高相等，即比较两三角形的底边长即可．
解答：设△ADC和△ABC的高为h，
S△ADC=
×AD×h，S△ABC=×BC×h，又AD=2cm，BC=5cm，
S△ADC：S△ABC=AD：BC=2：5．
故选A．
点评：本题考查了梯形的知识，难度不大，观察出△ADC和△ABC的高相等是关键．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
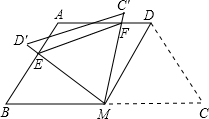如图，等腰梯形ABCD中，AD∥BC，AD=AB=CD=2，∠C=60°，M是BC的中点．
DE．
如图，在梯形ABCD中，AD∥BC，AB=CD，点E在BC的延长线上，且∠BDE=∠ADC．求证：AB•BD=DE•AD．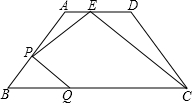
如图，在等腰梯形ABCD中，AD∥BC，AB=5，AD=6，BC=12，点E在AD边上，且AE：ED=1：2，点P是AB边上的一个动点，（P不与A，B重合）过点P作PQ∥CE交BC于点Q，设AP=x，CQ=y，则y与x之间的函数关系是
分别交边CD、BC于点F、E，若AD=3，BC=12，