题目内容
(1997•西宁)已知二次函数y=ax2+bx+c的图象抛物线G经过(-5,0),(0,
),(1,6)三点,直线l的解析式为y=2x-3
(1)求抛物线G的函数解析式;
(2)求证:抛物线G与直线L无公共点;
(3)若与l平行的直线y=2x+m与抛物线G只有一个公共点P,求P点的坐标.
| 5 | 2 |
(1)求抛物线G的函数解析式;
(2)求证:抛物线G与直线L无公共点;
(3)若与l平行的直线y=2x+m与抛物线G只有一个公共点P,求P点的坐标.
分析:(1)直接把点(-5,0),(0,
),(1,6)代入二次函数y=ax2+bx+c,求出a、b、c的值即可;
(2)把(1)中求出的抛物线的解析式与直线l的解析式y=2x-3组成方程组,再根据一元二次方程根的判别式即可得出结论;
(3)把直线y=2x+m与抛物线G的解析式组成方程组,根据只有一个公共点P可知△=0,求出m的值,故可得出P点坐标即可.
| 5 |
| 2 |
(2)把(1)中求出的抛物线的解析式与直线l的解析式y=2x-3组成方程组,再根据一元二次方程根的判别式即可得出结论;
(3)把直线y=2x+m与抛物线G的解析式组成方程组,根据只有一个公共点P可知△=0,求出m的值,故可得出P点坐标即可.
解答:解:(1)∵次函数y=ax2+bx+c的图象抛物线G经过(-5,0),(0,
),(1,6)三点,
∴
,解得
,
∴抛物线G的函数解析式为:y=
x2+3x+
;
(2)∵由(1)得抛物线G的函数解析式为:y=
x2+3x+
,
∴
,
①-②得,
x2+x+
=0,
∵△=12-4×
×
=-10<0,
∴方程无实数根,即抛物线G与直线L无公共点;
(3)∵与l平行的直线y=2x+m与抛物线G只有一个公共点P,
∴
,消去y得,
x2+x+
-m=0①,
∵抛物线G与直线y=2x+m只有一个公共点P,
∴△=12-4×
×(
-m)=0,解得m=2,
把m=2代入方程①得,
x2+x+
-2=0,解得x=-1,
把x=-1代入直线y=2x+2得,y=0,
∴P(-1,0).
| 5 |
| 2 |
∴
|
|
∴抛物线G的函数解析式为:y=
| 1 |
| 2 |
| 5 |
| 2 |
(2)∵由(1)得抛物线G的函数解析式为:y=
| 1 |
| 2 |
| 5 |
| 2 |
∴
|
①-②得,
| 1 |
| 2 |
| 11 |
| 2 |
∵△=12-4×
| 1 |
| 2 |
| 11 |
| 2 |
∴方程无实数根,即抛物线G与直线L无公共点;
(3)∵与l平行的直线y=2x+m与抛物线G只有一个公共点P,
∴
|
| 1 |
| 2 |
| 5 |
| 2 |
∵抛物线G与直线y=2x+m只有一个公共点P,
∴△=12-4×
| 1 |
| 2 |
| 5 |
| 2 |
把m=2代入方程①得,
| 1 |
| 2 |
| 5 |
| 2 |
把x=-1代入直线y=2x+2得,y=0,
∴P(-1,0).
点评:本题考查的是二次函数综合题,熟知待定系数法求一元二次方程的解析式及一元二次方程的解与△的关系式解答此题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
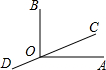 (1997•西宁)如图,已知∠AOB是直角,C、O、D三点共线,∠AOC=25°,则∠AOC的余角的补角为
(1997•西宁)如图,已知∠AOB是直角,C、O、D三点共线,∠AOC=25°,则∠AOC的余角的补角为