题目内容
 在矩形纸片ABCD中,AB=3cm,BC=4cm,现将纸片折叠压平,使A与C重合,如果设折痕为EF,那么重叠部分△AEF的面积等于
在矩形纸片ABCD中,AB=3cm,BC=4cm,现将纸片折叠压平,使A与C重合,如果设折痕为EF,那么重叠部分△AEF的面积等于
- A.

- B.
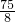
- C.

- D.
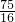
D
分析:要求重叠部分△AEF的面积,选择AF作为底,高就等于AB的长;而由折叠可知∠AEF=∠CEF,由平行得∠CEF=∠AFE,代换后,可知AE=AF,问题转化为在Rt△ABE中求AE.
解答:设AE=x,由折叠可知,EC=x,BE=4-x,
在Rt△ABE中,AB2+BE2=AE2,即32+(4-x)2=x2,
解得:x= ;
;
由折叠可知∠AEF=∠CEF,由AD∥BC得∠CEF=∠AFE,
∴∠AEF=∠AFE,即AE=AF= ;
;
∴S△AEF= ×AF×AB=
×AF×AB= ×
× ×3=
×3=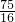 .故选D.
.故选D.
点评:本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.
分析:要求重叠部分△AEF的面积,选择AF作为底,高就等于AB的长;而由折叠可知∠AEF=∠CEF,由平行得∠CEF=∠AFE,代换后,可知AE=AF,问题转化为在Rt△ABE中求AE.
解答:设AE=x,由折叠可知,EC=x,BE=4-x,
在Rt△ABE中,AB2+BE2=AE2,即32+(4-x)2=x2,
解得:x=
 ;
;由折叠可知∠AEF=∠CEF,由AD∥BC得∠CEF=∠AFE,
∴∠AEF=∠AFE,即AE=AF=
 ;
;∴S△AEF=
 ×AF×AB=
×AF×AB= ×
× ×3=
×3=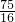 .故选D.
.故选D.点评:本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
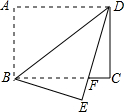 在矩形纸片ABCD中,AB=6,BC=8.将矩形纸片沿BD折叠,使点A落在点E处,设DE与BC相交于点F,求BF的长.
在矩形纸片ABCD中,AB=6,BC=8.将矩形纸片沿BD折叠,使点A落在点E处,设DE与BC相交于点F,求BF的长.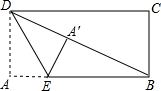 (2013•太原)如图,在矩形纸片ABCD中,AB=12,BC=5,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A′处,则AE的长为
(2013•太原)如图,在矩形纸片ABCD中,AB=12,BC=5,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A′处,则AE的长为 (2013•黄石模拟)如图,在矩形纸片ABCD中,AB=3,BC=4.把△BCD沿对角线BD折叠,使点C落在E处,BE交AD于点F;
(2013•黄石模拟)如图,在矩形纸片ABCD中,AB=3,BC=4.把△BCD沿对角线BD折叠,使点C落在E处,BE交AD于点F; 如图,在矩形纸片ABCD中,AB=6,BC=8,现将其沿EF对折,使得点C与点A重合,则AF的长为
如图,在矩形纸片ABCD中,AB=6,BC=8,现将其沿EF对折,使得点C与点A重合,则AF的长为 动手操作:如图,在矩形纸片ABCD中,AB=3,AD=5.如图所示折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动.
动手操作:如图,在矩形纸片ABCD中,AB=3,AD=5.如图所示折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动.