Question

某商业公司为指导某种应季商品的生产和销售，对三月份至七月份该商品的售价和生产进行了调研，结果如下：一件商品的售价M(元)与时间t(月)的关系可用一条线段上的点来表示(如图A)；一件商品的成本Q(元)与时间t(月)的关系可用一条抛物线上的点来表示，其中6月份成本最高(如图B)．

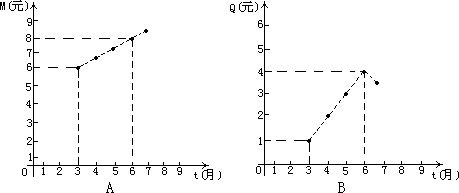
根据图像提供的信息解答下面问题：

(1)一件商品在3月份出售时的利润是多少元？(利润＝售价－成本)

(2)求图B中表示的一件商品的成本Q(元)与时间t(月)之间的函数关系式；

(3)你能求出三月份至七月份一件商品的利润W(元)与时间t(月)之间的函数关系式吗？若该公司能在一个月内售出此种商品30000件，请你计算一下该公司在一个月内最少获利多少元？

Answer 1

答案：
解析：

解：(1)由图像知，一件商品在3月份出售时的利润为5元． 　　(2)由图知，抛物线的顶点为(6，4)． 　　故设抛物线的解析式为Q=a(t－6)2＋4. 　　∵抛物线过(3，1)点，∴a(3－6)2+4=1.解得a=－． 　　即抛物线的解析式为Q=(t－6)2＋4=t2－4t－8．其中t=3，4，5，6，7． 　　(3)设每件商品的售价M(元)与时间t(月)之间的函数关系式为M=kt＋b． 　　∵线段过(3，6)，(6，8)两点，∴，解得，∴M=t+4，其中t=3，4，5，6，7． 　　∴一件商品的利润W(元)与时间t(月)的函数关系式为W=M－Q=(t+4)－(－t2+4t－8)=t2－+12． 　　W=(t－5)2＋，其中t=3，4，，5，6，7．当t=5时，W的最小值为元． 　　∴30000件商品一个月内售完至少获利30 000×=110000(元)． 　　答：该公司在一个月内最少获利110000元．