题目内容
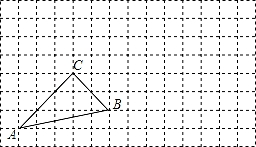
如图,点A在x轴上,OA=6,将线段OA绕点O顺时针旋转120°至OB的位置.
(1)求点B的坐标;
(2)求经过A、O、B的抛物线的解析式;
(3)在此抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形的面积是9?若存在,求出过点P的坐标;若不存在,请说明理由.
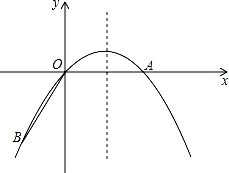
【考点】二次函数综合题.
【分析】(1)根据旋转的性质,可得OB=OA=6,∠BOC=120°,根据直角三角形的性质,可得BC,OC的长;
(2)根据抛物线与x轴的交点坐标,可得抛物线的解析式,根据待定系数法,可得答案;
(3)根据三角形的面积,可得P到BC的距离为3,根据平行线间的距离相等,可得平行OB且到OB的距离等于3的两条直线,根据自变量与函数值的对应关系,可得P点坐标.
【解答】解:(1)如图1:
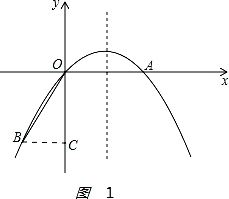
由OA=6,将线段OA绕点O顺时针旋转120°至OB的位置,得
OB=OA=6,∠BOC=120°.
∠BOC=120°﹣90°=30°
∴BC=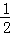 OB=3,
OB=3,
OC=3 ,
,
∴B(﹣3,﹣3 )
)
(2)因为抛物线与x轴交于O、A(6,0),
设抛物线的解析式为y=ax(x﹣6),把点B(﹣3,﹣3 )代入得﹣3a(﹣3﹣6)=﹣3
)代入得﹣3a(﹣3﹣6)=﹣3 ,
,
解得:a=﹣ .
.
所以抛物线的解析式为y=﹣ x(x﹣6)=﹣
x(x﹣6)=﹣ x2+
x2+ x.
x.
(3)答:符合条件的点P存在
设直线OB的解析式为:y=kx,
把点了B(﹣3,﹣3 )代入解得:k=
)代入解得:k=
∴直线OB的解析式为:y= x,
x,
∵S△BOP=9,
∴点P到OB的距离是:(9×2)÷6=3
如图2:

设点E到OB的距离EF=3,
∵∠BOE=30°,
∴OE=2EF=6
∴到直线OB的距离为3的直线解析式分别是:y= x﹣6 或y=
x﹣6 或y= x+6
x+6
抛物线的对称轴是直线x=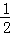 ×6=3,
×6=3,
∴把x=3分别代入y= x﹣6、y=
x﹣6、y= x+6得y 1=3
x+6得y 1=3 ﹣6,y 2=3
﹣6,y 2=3 +6,
+6,
即符合条件的点P的坐标是:P1(3,3 ﹣6),P2(3,3
﹣6),P2(3,3 +6).
+6).
【点评】本题考查了二次函数综合题,(1)利用了旋转的性质,直角三角形的性质;(2)利用待定系数法求函数解析式,关键是设出与X轴交点的解析式;(3)利用平行线间的距离相等得出平行OB且到OB的距离等于3的两条直线是解题关键.


 B.
B.
 C.
C.
 .
.
 的系数是3 D.
的系数是3 D. 不是多项式
不是多项式
 .
.