题目内容
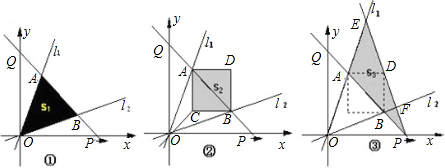
 如图,单位正方形ABCD被EF、GH分成相等的矩形.试问:是否存在另外的分法,既能将单位正方形分成面积相等的三个多边形,又能使三个多边形的公共边界小于EF与GH的和.
如图,单位正方形ABCD被EF、GH分成相等的矩形.试问:是否存在另外的分法,既能将单位正方形分成面积相等的三个多边形,又能使三个多边形的公共边界小于EF与GH的和.
解:如图,


设正方形ABCD的边长为1,
由于分成三面积相等,可以计算得出EF+GH=1+ =
= ,
,
存在,
假如能作出符合条件的图形如图(2),
设GH∥AD,延长HG交AB于N,过E作EQ⊥NH于Q,GH=x,
由梯形的面积公式得: (x+DE)•
(x+DE)• =
= ,
,
即:DE= -x,
-x,
∴AE=1-( -x)=-
-x)=- +x,
+x,
QG=1-(- +x)-x=
+x)-x= -2x,
-2x,
又∵EQ= ,
,
在△EQG中由勾股定理得:EG= ,
,
同理:FG= ,
,
GH+EG+GF=x+2 <
< ,
,
解得:0<x< ,
,
只要符合上面条件的GH的值都能画出,
故答案为:存在.
分析:首先设出正方形ABCD的边长为1,计算出EF+GH的值为 ,再进一步利用三部分面积相等求出三部分的面积为
,再进一步利用三部分面积相等求出三部分的面积为 ,设GH∥AD且GH=x,根据勾股定理求出EG 和FG的长度,根据GH+EG+GF<
,设GH∥AD且GH=x,根据勾股定理求出EG 和FG的长度,根据GH+EG+GF< 求出x的范围即可进行判断.
求出x的范围即可进行判断.
点评:此题主要利用正方形的性质,梯形的面积公式,勾股定理等知识,能正确利用知识进行计算是解此题的关键.


设正方形ABCD的边长为1,
由于分成三面积相等,可以计算得出EF+GH=1+
 =
= ,
,存在,
假如能作出符合条件的图形如图(2),
设GH∥AD,延长HG交AB于N,过E作EQ⊥NH于Q,GH=x,
由梯形的面积公式得:
 (x+DE)•
(x+DE)• =
= ,
,即:DE=
 -x,
-x,∴AE=1-(
 -x)=-
-x)=- +x,
+x,QG=1-(-
 +x)-x=
+x)-x= -2x,
-2x,又∵EQ=
 ,
,在△EQG中由勾股定理得:EG=
 ,
,同理:FG=
 ,
,GH+EG+GF=x+2
 <
< ,
,解得:0<x<
 ,
,只要符合上面条件的GH的值都能画出,
故答案为:存在.
分析:首先设出正方形ABCD的边长为1,计算出EF+GH的值为
 ,再进一步利用三部分面积相等求出三部分的面积为
,再进一步利用三部分面积相等求出三部分的面积为 ,设GH∥AD且GH=x,根据勾股定理求出EG 和FG的长度,根据GH+EG+GF<
,设GH∥AD且GH=x,根据勾股定理求出EG 和FG的长度,根据GH+EG+GF< 求出x的范围即可进行判断.
求出x的范围即可进行判断.点评:此题主要利用正方形的性质,梯形的面积公式,勾股定理等知识,能正确利用知识进行计算是解此题的关键.

练习册系列答案
相关题目
 23、如图(单位:m),直角梯形ABCD以2m/s的速度沿直线l向正方形CEFG方向移动,直到AB与FE重合,直角梯形ABCD与正方形CEFG重叠部分的面积S关于移动时间t的函数图象可能是( )
23、如图(单位:m),直角梯形ABCD以2m/s的速度沿直线l向正方形CEFG方向移动,直到AB与FE重合,直角梯形ABCD与正方形CEFG重叠部分的面积S关于移动时间t的函数图象可能是( )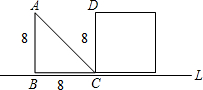 AB与CD重合.设x秒时,三角形与正方形不重叠部分的面积为ym2.
AB与CD重合.设x秒时,三角形与正方形不重叠部分的面积为ym2.
 如图,平移正方形网格中的阴影图案,使AB移到A′B′位置,画出平移后的图形,再将所得到的图形,向左平移9个单位长度.(设每1格代表1个单位长度)
如图,平移正方形网格中的阴影图案,使AB移到A′B′位置,画出平移后的图形,再将所得到的图形,向左平移9个单位长度.(设每1格代表1个单位长度)