Question

如图，抛物线y=ax²-4ax+b的顶点的纵坐标为3，且经过（0，2），交x轴于A、B（A在B左边）
（1）求此抛物线的解析式；
（2）设D为抛物线的顶点，点C关于x轴的对称点为E，x轴上一点M，使S_△MCE=S_△MCD，求M的坐标；
（3）将直线CD向下平移，交x、y轴分别于S、T，交抛物线于P，若

PS

PT

=2，求P点的坐标．

Answer 1

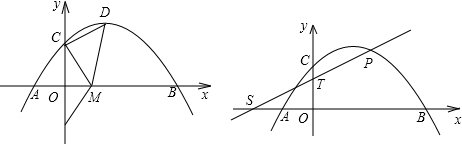
分析：（1）首先求出顶点坐标，利用待定的系数法求得物线的解析式；
（2）设出点M的坐标，由三角形的面积计算方法联立方程即可解答；
（3）求出直线CD，进一步得到直线PS的解析式，由此联立一元二次方程求得结果．

解答：解：（1）抛物线y=ax²-4ax+b的对称轴是x=-

-4a

2a

=2，顶点坐标为（2，3），且经过C（0，2），
代入函数解析式得

4a-8a+b=3 b=2

，
解得

a= 1 4 b=2

，
所以函数解析式为y=-

1

4

x2+x+2；

（2）如图，

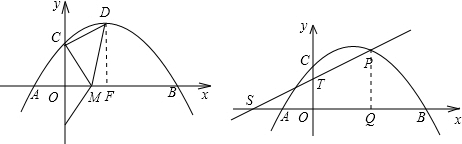
作DF垂直于x轴，垂足为F，
由题意知C（0，2），D（2，3），E（0，-2），F（0，2），设M点坐标为（x，0），
由S_△MCE=S_△MCD得

1

2

×4x=

1

2

（2+3）×2-

1

2

×2x-

1

2

（2-x）×3，
解得x=

4

3

，所以点M坐标为（

4

3

，0），点M关于y轴的对称点（-

4

3

，0）也符合要求，
所以M的坐标为M(±

4

3

，0)；

（3）如上图，设P点坐标为（x，-

1

4

x2+x+2），过点P作PQ⊥x轴，垂足为Q，
可得到△SOT∽△SQP，

PQ

TO

=

PS

ST

，又因

PS

PT

=2，所以

PQ

TO

=2，
因此T点坐标为（0，-

1

8

x2+

1

2

x+1），
经过C、D两点直线CD的解析式为y=

1

2

x+2，
因此直线PS的解析式为y=

1

2

x+（-

1

8

x²+

1

2

x+1）=-

1

8

x²+x+1，与抛物线联立方程得，
-

1

4

x²+x+2=-

1

8

x²+x+1，解得x=±2

2

，
代入抛物线解析式可得y=2

2

，
因此P点坐标为P(±2

2

，2

2

)．

点评：此题考查待定系数法求函数解析式，二次函数图象上点的坐标特征，三角形相似的判定与性质，三角形的面积等内容．