题目内容
已知在△ABC中,BC=a.如图1,点B1、C1分别是AB、AC的中点,则线段B1C1的长是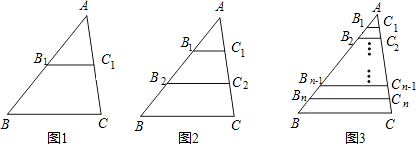
分析:先根据三角形的中位线定理得出B1C1的长,再作图2中三角形的中位线,根据三角形的中位线定理和梯形的中位线定理推得B1C1+B2C2的值,依此类推得出B1C1+B2C2+B3C3的值,从而得出B1C1+B2C2+…+BnCn的值.
解答:解:∵点B1、C1分别是AB、AC的中点,
∴B1C1=
BC=
a,
作图2中三角形的中位线MN,则MN=
a,
则B1C1=
a①,B2C2=
a②,
①+②得,B1C1+B2C2=
a+
a=a,
同理得出B1C1+B2C2+B3C3=
a+
a+
a=
a,
…
B1C1+B2C2+…+BnCn=
na.
故答案为
na.
∴B1C1=
| 1 |
| 2 |
| 1 |
| 2 |
作图2中三角形的中位线MN,则MN=
| 1 |
| 2 |
则B1C1=
| 1 |
| 3 |
| 2 |
| 3 |
①+②得,B1C1+B2C2=
| 1 |
| 3 |
| 2 |
| 3 |
同理得出B1C1+B2C2+B3C3=
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
…
B1C1+B2C2+…+BnCn=
| 1 |
| 2 |
故答案为
| 1 |
| 2 |
点评:本题是一道规律性的题目,考查了三角形的中位线定理以及梯形的中位线定理,是基础知识要熟练掌握.

练习册系列答案
相关题目
 22、如图,已知在△ABC中,∠A=(2x+10)°,∠B=(3x)°,∠ACD是△ABC的一个外角,且∠ACD=(6x-10)°,求∠A的度数.
22、如图,已知在△ABC中,∠A=(2x+10)°,∠B=(3x)°,∠ACD是△ABC的一个外角,且∠ACD=(6x-10)°,求∠A的度数.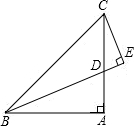 如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E.若BD平分∠ABC.
如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E.若BD平分∠ABC. 如图,已知在△ABC中,∠B与∠C的平分线交于点P.
如图,已知在△ABC中,∠B与∠C的平分线交于点P.