题目内容
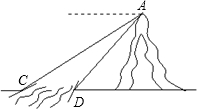如图，小山脚下有一条小河，从山顶A处测得河对岸点C的俯角为30°，测得岸边点D的俯角为45°，又知河宽CD为50米．现需从山顶A到河岸点C拉一条笔直的缆绳AC，求缆绳AC的长．（精确到0.1米，
| 2 |
| 3 |
分析：过A作AB⊥CD，根据三角函数可以证明AB=BD，在直角△ACB中，根据三角函数的定义即可得到关于AB的方程，即可求解．
解答：
解：过A作AB⊥CD，∠ACB=30°，∠ADB=45°
设AB=BD=x
tan∠ACB=
tan30°=
，
=
x=25
+25
AC=2AB=50+50
≈136.5
答：缆绳AC的长为136.5米．
解：过A作AB⊥CD，∠ACB=30°，∠ADB=45°设AB=BD=x
tan∠ACB=
| AB |
| CB |
tan30°=
| x |
| 50+x |
| ||
| 3 |
| x |
| 50+x |
| 3 |
AC=2AB=50+50
| 3 |
答：缆绳AC的长为136.5米．
点评：本题考查仰角的定义，要求学生能借助仰角构造直角三角形并解直角三角形．在解题的过程中注意两个直角三角形之间的联系．
练习册系列答案
相关题目
如图，小山脚下有一条小河，从山顶A处测得河对岸点C的俯角为30°，测得岸边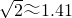
，
）
，
）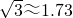