题目内容
设关于x的方程ax2+(a+2)x+9a=0有两个不相等的实数根x1、x2,且x1<2<x2,那么实数a的取值范围是________.
- <a<0
<a<0
分析:根据根的判别式求出a的取值范围,再根据根与系数的关系求出a的取值范围,求其公共解即可.
解答:∵关于x的方程ax2+(a+2)x+9a=0有两个不相等的实数根x1、x2,
∴△=(a+2)2-4a•9a=a2+4a+4-36a2=-35a2+4a+4>0;
整理得(-5a+2)(7a+2)>0,
即 ,解得-
,解得- <a<
<a< ;
;
或 ,无解;
,无解;
又∵x1<2<x2,
∴x1-2<0,x2-2>0,
∴(x1-2)(x2-2)<0,
即x1x2-2(x1+x2)+4<0,
根据根与系数的关系得,9-2×(-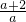 )+4<0,
)+4<0,
解得0>a>- ,
,
综上,- <a<0.
<a<0.
故答案为- <a<0.
<a<0.
点评:此题考查了一元二次方程根的判别式及根与系数的关系,将二者结合是解题常用的方法.
 <a<0
<a<0分析:根据根的判别式求出a的取值范围,再根据根与系数的关系求出a的取值范围,求其公共解即可.
解答:∵关于x的方程ax2+(a+2)x+9a=0有两个不相等的实数根x1、x2,
∴△=(a+2)2-4a•9a=a2+4a+4-36a2=-35a2+4a+4>0;
整理得(-5a+2)(7a+2)>0,
即
 ,解得-
,解得- <a<
<a< ;
;或
 ,无解;
,无解;又∵x1<2<x2,
∴x1-2<0,x2-2>0,
∴(x1-2)(x2-2)<0,
即x1x2-2(x1+x2)+4<0,
根据根与系数的关系得,9-2×(-
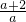 )+4<0,
)+4<0,解得0>a>-
 ,
,综上,-
 <a<0.
<a<0.故答案为-
 <a<0.
<a<0.点评:此题考查了一元二次方程根的判别式及根与系数的关系,将二者结合是解题常用的方法.

练习册系列答案
相关题目
设关于x的方程ax2+(a+2)x+9a=0,有两个不相等的实数根x1、x2,且x1<1<x2,那么实数a的取值范围是( )
A、a<-
| ||||
B、
| ||||
C、a>
| ||||
D、-
|











