题目内容
解方程: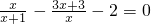
解:设y= ,则原方程化为y-
,则原方程化为y-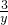 -2=0,
-2=0,
∴y2-2y-3=0,
解得:y1=3,y2=-1.
当y1=3时, =3,解得x1=-
=3,解得x1=- ;
;
当y2=-1时, =-1,解得x2=-
=-1,解得x2=- .
.
经检验,原方程的解是x1=- ,x2=-
,x2=- .
.
分析:此题用换元法解答,设y= ,把分式方程化为整式方程求解.
,把分式方程化为整式方程求解.
点评:(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.
(2)解分式方程一定注意要验根.
 ,则原方程化为y-
,则原方程化为y-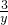 -2=0,
-2=0,∴y2-2y-3=0,
解得:y1=3,y2=-1.
当y1=3时,
 =3,解得x1=-
=3,解得x1=- ;
;当y2=-1时,
 =-1,解得x2=-
=-1,解得x2=- .
.经检验,原方程的解是x1=-
 ,x2=-
,x2=- .
.分析:此题用换元法解答,设y=
 ,把分式方程化为整式方程求解.
,把分式方程化为整式方程求解.点评:(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.
(2)解分式方程一定注意要验根.

练习册系列答案
 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目