题目内容
已知抛物线 (m为整数)与x轴交于点A,与y轴交于点B,且OA=OB,则m等于
(m为整数)与x轴交于点A,与y轴交于点B,且OA=OB,则m等于
- A.

- B.

- C.2
- D.-2
D
分析:易得抛物线与y轴的交点,那么可得到与x轴的交点坐标,代入函数即可求得m的值.
解答:∵当x=0时,y= m2-1
m2-1
∴抛物线与y轴的交点B为(0, m2-1),
m2-1),
∵OA=OB
∴抛物线与x轴的交点A为( m2-1,0)或(
m2-1,0)或( m2+1,0),
m2+1,0),
∴( m2-1)2+(m+1)(
m2-1)2+(m+1)( m2-1)
m2-1) m2-1=0或(
m2-1=0或( m2+1)2+(m+1)(
m2+1)2+(m+1)( m2+1)-
m2+1)- m2-1=0,
m2-1=0,
∴ m2-1=0或
m2-1=0或 m2-1+m+1+1=0或
m2-1+m+1+1=0或 m2+1=0或
m2+1=0或 m2+1+m+1-1=0,
m2+1+m+1-1=0,
∵m为整数
∴m=-2.
故选D.
点评:此题考查了二次函数的性质,考查了二次函数与x轴、y轴的交点坐标,当x=0时,求得二次函数与y轴的交点,当y=0时,求得二次函数与x轴的交点.
分析:易得抛物线与y轴的交点,那么可得到与x轴的交点坐标,代入函数即可求得m的值.
解答:∵当x=0时,y=
 m2-1
m2-1∴抛物线与y轴的交点B为(0,
 m2-1),
m2-1),∵OA=OB
∴抛物线与x轴的交点A为(
 m2-1,0)或(
m2-1,0)或( m2+1,0),
m2+1,0),∴(
 m2-1)2+(m+1)(
m2-1)2+(m+1)( m2-1)
m2-1) m2-1=0或(
m2-1=0或( m2+1)2+(m+1)(
m2+1)2+(m+1)( m2+1)-
m2+1)- m2-1=0,
m2-1=0,∴
 m2-1=0或
m2-1=0或 m2-1+m+1+1=0或
m2-1+m+1+1=0或 m2+1=0或
m2+1=0或 m2+1+m+1-1=0,
m2+1+m+1-1=0,∵m为整数
∴m=-2.
故选D.
点评:此题考查了二次函数的性质,考查了二次函数与x轴、y轴的交点坐标,当x=0时,求得二次函数与y轴的交点,当y=0时,求得二次函数与x轴的交点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
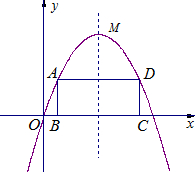 .其顶点M在第一象限.
.其顶点M在第一象限. (m为整数)与x轴交于点A,与y轴交于点B,且OA=OB,则m等于( )
(m为整数)与x轴交于点A,与y轴交于点B,且OA=OB,则m等于( )
