Question

已知正方形纸片ABCD的边长为2．
操作：如图1，将正方形纸片折叠，使顶点A落在边CD上的点P处(点P与C、D不重合)，折痕为EF，折叠后AB边落在PQ的位置，PQ与BC交于点G．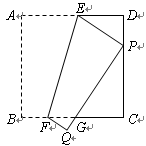

探究：【小题1】(1)观察操作结果，找到一个与△DEP相似的三角形，并证明你的结论；
【小题2】(2)当点P位于CD中点时，你找到的三角形与△DEP周长的比是多少？

Answer 1

【小题1】(1) 与相似．……………1分
证明：∵四边形ABCD是正方形，
∴∠A＝∠C＝∠D＝90°．
由折叠知 ∠EPQ＝∠A＝90°．
∴∠PED+∠DPE＝90°，∠DPE+∠CPG＝90°．
∴∠PED＝∠CPG．
∴∽．
【小题2】(2)设ED＝x，则AE＝，
由折叠可知：EP＝AE＝．
∵点P是CD中点，∴DP＝1．
∵∠D＝90°，∴， ……………8分
即解得 ．∴．……………………………10分
∵∽，∴．∴与周长的比为4∶3

解析