题目内容
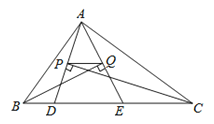
【题目】如图，△ABC中AC=BC，点D，E在AB边上，连接CD，CE．
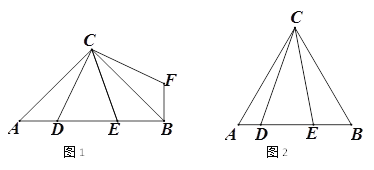
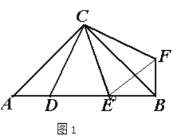
(1)如图1，如果∠ACB=90°，把线段CD逆时针旋转90°，得到线段CF，连接BF，
①求证：△ACD≌△BCF；
②若∠DCE=45°， 求证：DE2=AD2+BE2；
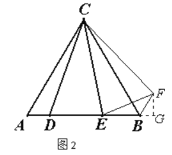
(2)如图2，如果∠ACB=60°，∠DCE=30°，用等式表示AD，DE，BE三条线段的数量关系，说明理由．
【答案】（1）①详见解析；②详见解析；（2）DE2= EB2+AD2+EB·AD，证明详见解析
【解析】
（1）①根据旋转的性质可得CF=CD，∠DCF=90°，再根据已知条件即可证明△ACD≌△BCF；
②连接EF，根据①中全等三角形的性质可得∠EBF=90°，再证明△DCE≌△FCE得到EF=DE即可证明；
（2）根据（1）中的思路作出辅助线，通过全等三角形的判定及性质得出相等的边，再由勾股定理得出AD，DE，BE之间的关系．
解：（1）①证明：由旋转可得CF=CD，∠DCF=90°
∵∠ACD=90°
∴∠ACD=∠BCF
又∵AC=BC
∴△ACD≌△BCF
②证明：连接EF，
由①知△ACD≌△BCF
∴∠CBF=∠CAD=∠CBA=45°，∠BCF=∠ACD，BF=AD
∴∠EBF=90°
∴EF2=BE2+BF2，
∴EF2=BE2+AD2
又∵∠ACB=∠DCF=90°，∠CDE=45°
∴∠FCE=∠DCE=45°
又∵CD=CF，CE=CE
∴△DCE≌△FCE
∴EF=DE
∴DE2= AD2+BE2
⑵DE2= EB2+AD2+EB·AD
理由：如图2，将△ADC绕点C逆时针旋转60°，得到△CBF，过点F作FG⊥AB，交AB的延长线于点G，连接EF，
∴∠CBE=∠CAD，∠BCF=∠ACD， BF=AD
∵AC=BC，∠ACB=60°
∴∠CAB=∠CBA =60°
∴∠ABE=120°，∠EBF=60°，∠BFG=30°
∴BG=
BF，FG=
BF
∵∠ACB=60°，∠DCE=30°，
∴∠ACD+∠BCE=30°，
∴∠ECF=∠FCB+∠BCE=30°
∵CD=CF，CE=CE
∴△ECF≌△ECD
∴EF=ED
在Rt△EFG中，EF2=FG2+EG2
又∵EG=EB+BG
∴EG=EB+BF，
∴EF2=（EB+BF）2+（BF）2
∴DE2= （EB+AD）2+（AD）2
∴DE2= EB2+AD2+EB·AD
