题目内容
 在边长为1的正方形网格中,有等腰Rt△ABC和半径为2的⊙O.
在边长为1的正方形网格中,有等腰Rt△ABC和半径为2的⊙O.
(1)将等腰Rt△ABC进行怎样的平移,使点A平移到点O的位置?请你描述出平移的过程,并画出平移后的△A′B′C′;
(2)在(1)的条件下,求出△A′B′C′和⊙O的重叠部分的面积;
(3)以点B′为位似中心,在网格中将Rt△ABC放大2倍,画出放大后的图形.
 解:(1)先将等腰Rt△ABC向上平移4个单位,再向右平移6个单位后,可使点A平移到点O的位置.
解:(1)先将等腰Rt△ABC向上平移4个单位,再向右平移6个单位后,可使点A平移到点O的位置.如图所示;
(2)∵△ABC是等腰直角三角形,
∴∠BAC=45°
又∵⊙O的半径为2,
∴S扇形=
 ,
,=
 л;
л;(3)如图所示;

分析:(1)利用平移的性质分别将三角形向上平移4个单位,再向右平移6个单位,即可得出符合要求的图案;
(2)根据等腰直角三角形的性质得出∠A′的度数,再利用扇形面积公式求出即可;
(3)利用位似图形性质与画法,找到A″,B″,C″即可得出符合要求的图形.
点评:此题主要考查了位似图形的画法以及图形的平移和扇形的面积公式等知识,此题考查知识便比较全面是比较典型的一个题目.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
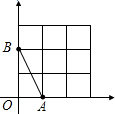 如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上.
如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上. 如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上.
如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上. 如图所示,在平面直角坐标系中,A、B、C、D均在边长为1的正方形网格格点上.
如图所示,在平面直角坐标系中,A、B、C、D均在边长为1的正方形网格格点上.
 (2)将线段
(2)将线段