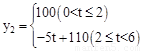题目内容
某公司生产的一种健身产品在市场上受到普遍欢迎，每年可在国内、国外市场上全部售完，该公司的年产量为6千件，若在国内市场销售，平均每件产品的利润y1（元）与国内销售数量x（千件）的关系为：
若在国外销售，平均每件产品的利润y2（元）与国外的销售数量t（千件）的关系为：
（1） 用x的代数式表示t为：t＝ ；当0＜x≤4时，
y2与x的函数关系为y2＝ ；当 ≤x＜ 时，y2＝100；
（2）求每年该公司销
售
这种健身产品的总利润w（千元）与国内的销售数量x（千件）的函数关系式，并指出x的取值范围；
（3）该公司每年国内、国外的销售量各为多少时，可使公司每年的总利润最大？最大值为多少？
解：（1）t＝6－x；当0＜x≤4时，y2＝－5(6－x)＋110＝5x＋80．
当4≤x＜6时，y2＝100．
（2）当0＜x≤2时，w＝(15x＋90)x＋(5x＋80)(6－x)＝10x2＋40x＋480；
当2＜x≤4时，w＝(－5x＋130)x＋(5x＋80)(6－x)＝－10x2＋80x＋480；
当4＜x＜6时，w＝(－5x＋130)x＋100(6－x)＝－5x2＋30x＋600；
（3）当0＜x≤2时，w＝10x2＋40x＋480＝10(x＋2)2＋440．此时x＝2时，w最大＝600．
当2＜x≤4时，w＝－10x2＋80x＋480＝－10(x－4)2＋640．x＝4时，w最大＝640．
当4＜x＜6时，w＝－5x2＋30x＋600＝－5(x－3)2＋645．4＜x＜6时，w＜640．
∴x＝4时，w最大＝640．
国内4千件，国外2千件，最大利润为64万元（或640千元）．
练习册系列答案
相关题目
y2=
若在国外销售，平均每件产品的利润y2（元）与国外的销售数量t（千件）的关系为：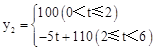
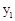（元）与国内销售数量
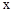（千件）的关系为：
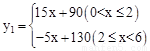若在国外销售，平均每件产品的利润
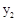（元）与国外的销售数量t（千件）的关系为：