Question

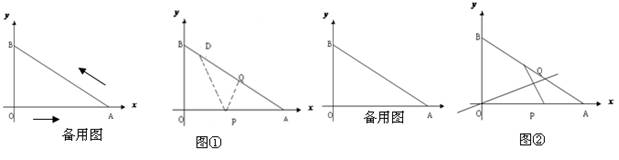
已知：如图，在直角梯形ABCD中，AD∥BC，∠B=90°，AD=2，BC=6，AB=3．E为BC边上一点，以BE为边作正方形BEFG，使正方形BEFG和梯形ABCD在BC的同侧．

（1）当正方形的顶点F恰好落在对角线AC上时，求BE的长；

（2）将（1）问中的正方形BEFG沿BC向右平移，记平移中的正方形BEFC为正方形B′EFG，当点E与点C重合时停止平移．设平移的距离为t，正方形B′EFG的边EF与AC交于点M，连接B′D，B′M，DM，是否存在这样的t，使△B′DM是直角三角形？若存在，求出t的值；若不存在，请说明理由；

（3）在（2）问的平移过程中，设正方形B′EFG与△ADC重叠部分的面积为S，请直接写出S与t之间的函数关系式以及自变量t的取值范围．

Answer 1

考点：相似三角形的判定与性质；勾股定理；正方形的性质；直角梯形。

解答：解：（1）如图①，

设正方形BEFG的边长为x，

则BE=FG=BG=x，

∵AB=3，BC=6，

∴AG=AB﹣BG=3﹣x，

∵GF∥BE，

∴△AGF∽△ABC，

∴，

即，

解得：x=2，

即BE=2；

（2）存在满足条件的t，

理由：如图②，过点D作DH⊥BC于H，

则BH=AD=2，DH=AB=3，

由题意得：BB′=HE=t，HB′=|t﹣2|，EC=4﹣t，

在Rt△B′ME中，B′M²=ME²+B′E²=2²+（2﹣t）²=t²﹣2t+8，

∵EF∥AB，

∴△MEC∽△ABC，

∴，即，

∴ME=2﹣t，

在Rt△DHB′中，B′D²=DH²+B′H²=3²+（t﹣2）²=t²﹣4t+13，

过点M作MN⊥DH于N，

则MN=HE=t，NH=ME=2﹣t，

∴DN=DH﹣NH=3﹣（2﹣t）=t+1，

在Rt△DMN中，DM²=DN²+MN²=t²+t+1，

（Ⅰ）若∠DB′M=90°，则DM²=B′M²+B′D²，

即t²+t+1=（t²﹣2t+8）+（t²﹣4t+13），

解得：t=，

（Ⅱ）若∠B′MD=90°，则B′D²=B′M²+DM²，

即t²﹣4t+13=（t²﹣2t+8）+（t²+t+1），

解得：t₁=﹣3+，t₂=﹣3﹣（舍去），

∴t=﹣3+；

（Ⅲ）若∠B′DM=90°，则B′M²=B′D²+DM²，

即：t²﹣2t+8=（t²﹣4t+13）+（t²+t+1），

此方程无解，

综上所述，当t=或﹣3+时，△B′DM是直角三角形；

（3）①如图③，当F在CD上时，EF：DH=CE：CH，

即2：3=CE：4，

∴CE=，

∴t=BB′=BC﹣B′E﹣EC=6﹣2﹣=，

∵ME=2﹣t，

∴FM=t，

当0≤t≤时，S=S_△FMN=×t×t=t²，

②当G在AC上时，t=2，

∵EK=EC•tan∠DCB=EC•=（4﹣t）=3﹣t，

∴FK=2﹣EK=t﹣1，

∵NL=AD=，

∴FL=t﹣，

∴当＜t≤2时，S=S_△FMN﹣S_△FKL=t²﹣（t﹣）（t﹣1）=﹣t²+t﹣；

③如图⑤，当G在CD上时，B′C：CH=B′G：DH，

即B′C：4=2：3，

解得：B′C=，

∴EC=4﹣t=B′C﹣2=，

∴t=，

∵B′N=B′C=（6﹣t）=3﹣t，

∵GN=GB′﹣B′N=t﹣1，

∴当2＜t≤时，S=S_梯形GNMF﹣S_△FKL=×2×（t﹣1+t）﹣（t﹣）（t﹣1）=﹣t²+2t﹣，

④如图⑥，当＜t≤4时，

∵B′L=B′C=（6﹣t），EK=EC=（4﹣t），B′N=B′C=（6﹣t）EM=EC=（4﹣t），

S=S_梯形MNLK=S_{梯形B′EKL}﹣S_{梯形B′EMN}=﹣t+．

综上所述：

当0≤t≤时，S=t²，

当＜t≤2时，S=﹣t²+t﹣；

当2＜t≤时，S=﹣t²+2t﹣，

当＜t≤4时，S=﹣t+．