题目内容
抛物线y=x2-3x-6的对称轴是直线
- A.
- B.
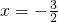
- C.x=3
- D.x=-3
A
分析：利用配方法将抛物线的一般式转化为顶点式，可确定顶点坐标和对称轴．
解答：∵y=x2-3x-6=x2-3x+
--6=（x-
）2-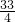
，
∴抛物线y=x2-3x-6的对称轴是直线x=．
故选A．
点评：此题考查了二次函数的性质，二次函数为y=a（x-h）2+k顶点坐标是（h，k），对称轴是x=h；此题还考查了配方法求顶点式．
分析：利用配方法将抛物线的一般式转化为顶点式，可确定顶点坐标和对称轴．
解答：∵y=x2-3x-6=x2-3x+
--6=（x-）2-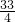，∴抛物线y=x2-3x-6的对称轴是直线x=
．故选A．
点评：此题考查了二次函数的性质，二次函数为y=a（x-h）2+k顶点坐标是（h，k），对称轴是x=h；此题还考查了配方法求顶点式．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
抛物线y=x2+3x的顶点在（ ）
| A、第一象限 | B、第二象限 | C、第三象限 | D、第四象限 |
如图，已知直线y=x+2与y轴交于点A，与抛物线y=-x2+3x+5交于B，C两点．
如图，抛物线y=-x2+3x-n经过点C（0，4），与x轴交于两点A、B．