Question

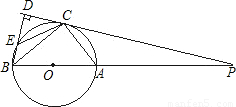
已知：如图，AB是⊙O的直径，点P为BA延长线上一点，PC为⊙O的切线，C为切点，BD⊥PC，垂足为D，交⊙O于E，连接AC、BC、EC．
（1）求证：BC²=BD•BA；
（2）若AC=6，DE=4，求PC的长．

Answer 1

【答案】分析：（1）要求证：BC²=BD•BA，可以转化为求证Rt△BDC∽Rt△BCA的问题；
（2）求PC的长，根据切割线定理得到PC²=PA•PB，可以转化为求AP，PB的问题，根据Rt△CED∽Rt△BAC和△PCA∽△PBC就可以求出．
解答：（1）证明：∵AB为⊙O的直径，
∴∠BCA=90°，
∵PC为⊙O的切线，
∴∠BCD=∠BAC，（1分）
∵BD⊥PD，
∴∠BDP=∠BCA=90，
∴Rt△BDC∽Rt△BCA，（1分）
∴，
∴BC²=BD•BA．（1分）

（2）解：∵Rt△BDC∽Rt△BCA，
∴∠DBC=∠CBA，
∴EC=AC，
∴EC=AC=6，
∵∠DBC=∠CBA，
∴∠DCE=∠CBA，
∴Rt△CED∽Rt△BAC，
∴，
∴AB=9，（1分）
由勾股定理得，
∵∠PCA=∠PBC，∠P=∠P，
∴△PCA∽△PBC，
∴，（1分）
设PA=6m，则PC=m，
由切割线定理得PC²=PA•PB，
∴45m²=6m（6m+9），
解得m=6，
∴PC=．（1分）
点评：命题立意：此题作为压轴题，综合考查圆的切线，三角形相似的判定与性质等知识．此题是一个大综合题，难度较大，有利于培养同学们的钻研精神和坚韧不拔的意志品质．