题目内容
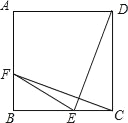
【题目】图①，图②都是4×6的正方形网格，每个小正方形的顶点称为格点，每个小正方形的边长均为1．在图①，图②中已画出线段AB，且点A，B均在格点上．
（1）在图①中以AB为对角线画出一个矩形，使矩形的另外两个顶点也在格点上，且所画的矩形不是正方形；
（2）在图②中以AB为对角线画出一个菱形，使菱形的另外两个顶点也在格点上，且所画的菱形不是正方形；
（3）图①中所画的矩形的面积为 ；图②中所画的菱形的周长为 ．
【答案】（1）见解析；（2）见解析；（3）8，4
．
【解析】
（1）根据矩形的性质画图即可；
（2）根据菱形的性质画图即可；
（3）根据矩形的面积公式和菱形的周长公式即可得到结论．
解：（1）如图①所示，矩形ACBD即为所求；
（2）如图②所示，菱形AFBE即为所求；
（3）矩形ACBD的面积=2×4=8；菱形AFBE的周长=4×
=4，
故答案为：8，4．
练习册系列答案
相关题目
【题目】某批乒乓球的质量检验结果如下：
抽取的乒乓球数n | 200 | 500 | 1000 | 1500 | 2000 |
优等品频数m | 188 | 471 | 946 | 1426 | 1898 |
优等品频率 | 0.940 | 0.942 | 0.946 | 0.951 | 0.949 |
（1）画出这批乒乓球“优等品”频率的折线统计图；
（2）这批乒乓球“优等品”的概率的估计值是多少？
（3）从这批乒乓球中选择5个黄球、13个黑球、22个红球，它们除颜色外都相同，将它们放入一个不透明的袋中．
①求从袋中摸出一个球是黄球的概率；
②现从袋中取出若干个黑球，并放入相同数量的黄球，搅拌均匀后使从袋中摸出一个是黄球的概率不小于
， 问至少取出了多少个黑球？
