题目内容
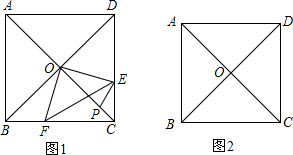
已知正方形ABCD,AC、BD交于O点,将一个三角板的直角顶点与O重合,它的两条直角边分别与AB、BC相交于点E、F.
(1)当三角板绕点O旋转到OE与AB垂直时(如图1),求证:BE+BF=![]() OB.
OB.
(2)当三角板在(1)的条件下绕点O逆时针旋转a°(0°<a<45°)时,如图2,上述结论是否成立?若成立,请给予证明;若不成立请说明理由.
 |
(1)∵ABCD是正方形,O为对角线AC、BD的交点,
∴OB=OC,OB⊥OC,BC=![]() OB.
OB.
又∵OE⊥AB,OF⊥BC,
∴OE=OF
∴Rt△BOE≌Rt△COF
∴BE=CF
∴BE+BF=CF+BF=![]() OB.
OB.
(2)BE+BF=![]() OB仍然成立
OB仍然成立
理由是:∵∠EOB+∠BOF=90°,∠COF+∠BOF=90°
∴∠EOB=∠COF
又OB=OC, ∠OBE=∠OCF=45°
∴△BOE≌△COF
∴BE=CF
∴BE+BF=CF+BF=![]() OB.
OB.

练习册系列答案
相关题目
 直至点G与点B重合为止.设x秒时Rt△EFG与正方形ABCD重叠部分的面积记为ycm2.
直至点G与点B重合为止.设x秒时Rt△EFG与正方形ABCD重叠部分的面积记为ycm2. 已知正方形ABCD的边长为4厘米,E,F分别为边DC,BC上的点,BF=1厘米,CE=2厘米,BE,DF相交于点G,求四边形CEGF的面积.
已知正方形ABCD的边长为4厘米,E,F分别为边DC,BC上的点,BF=1厘米,CE=2厘米,BE,DF相交于点G,求四边形CEGF的面积.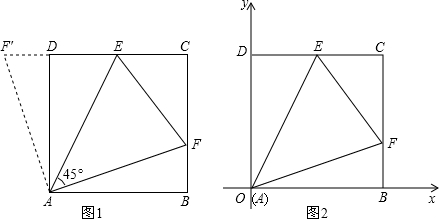
 如图,已知正方形ABCD边长为2,E、F、G、H分别为各边上的点,且AE=BF=CG=DH.
如图,已知正方形ABCD边长为2,E、F、G、H分别为各边上的点,且AE=BF=CG=DH.