题目内容
如图，若四边形ABCD是正方形，△CDE是等边三角形，则∠EAB的度数为________．
75°
分析：易证△ADE≌△BCE，则AE=BE，正方形中AD=DC，等边三角形中DC=DE，因此AD=DE，∵∠ADE=90°+60°=150°，∴∠DEA=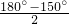
=15°，同理∠CEB=15°，∴∠AEB=60°-15°-15°=30°，即可求∠EAB的大小．
解答：∵∠ADE=∠BCE=90°+60°=150°，
AD=BC，DE=CE，
∴△ADE≌△BCE，
∴AE=BE，∴∠EAB=∠EBA．
∵正方形中AD=DC，等边三角形中DC=DE，
∴AD=DE，
∵∠ADE=90°+60°=150°，
∴∠DEA=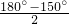=15°，同理∠CEB=15°，
∴∠AEB=60°-15°-15°=30°，
∴∠EAB=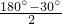
=75°．
故答案为 75°．
点评：本题考查了正方形各边长相等、各内角为直角的性质，考查了正三角形各边长相等、各内角为60°的性质，考查了等腰三角形底角相等的性质，本题中求证∠DEA=∠CEB=15°是解题的关键．
分析：易证△ADE≌△BCE，则AE=BE，正方形中AD=DC，等边三角形中DC=DE，因此AD=DE，∵∠ADE=90°+60°=150°，∴∠DEA=
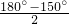=15°，同理∠CEB=15°，∴∠AEB=60°-15°-15°=30°，即可求∠EAB的大小．解答：∵∠ADE=∠BCE=90°+60°=150°，
AD=BC，DE=CE，
∴△ADE≌△BCE，
∴AE=BE，∴∠EAB=∠EBA．
∵正方形中AD=DC，等边三角形中DC=DE，
∴AD=DE，
∵∠ADE=90°+60°=150°，
∴∠DEA=
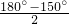=15°，同理∠CEB=15°，∴∠AEB=60°-15°-15°=30°，
∴∠EAB=
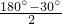=75°．故答案为 75°．
点评：本题考查了正方形各边长相等、各内角为直角的性质，考查了正三角形各边长相等、各内角为60°的性质，考查了等腰三角形底角相等的性质，本题中求证∠DEA=∠CEB=15°是解题的关键．
练习册系列答案
云南师大附小一线名师提优作业系列答案
相关题目
19、如图，若将△ABC沿CA方向平移CA长得△EFA，若△ABC的面积为3cm2，则四边形BCEF的面积是
