题目内容
在△ABC中,AB=AC,∠BAC=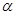 (
(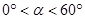 ),将线段BC绕点B逆时针旋转60°得到线段BD.
),将线段BC绕点B逆时针旋转60°得到线段BD.
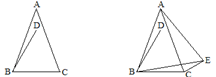
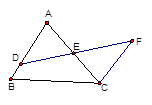
(1)如图1,直接写出∠ABD的大小(用含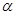 的式子表示);
的式子表示);
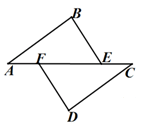
(2)如图2,∠BCE=150°,∠ABE=60°判断△ABE的形状并加以证明;
(3)在(2)的条件下,连结DE,若∠DEC=45°,求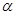 的值。
的值。
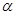 (
(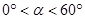 ),将线段BC绕点B逆时针旋转60°得到线段BD.
),将线段BC绕点B逆时针旋转60°得到线段BD.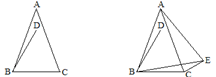
(1)如图1,直接写出∠ABD的大小(用含
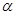 的式子表示);
的式子表示);(2)如图2,∠BCE=150°,∠ABE=60°判断△ABE的形状并加以证明;
(3)在(2)的条件下,连结DE,若∠DEC=45°,求
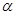 的值。
的值。(1)∠ABD=30°- a;(2)△ABE是等边三角形(证明见解析);(3)a=30°.
a;(2)△ABE是等边三角形(证明见解析);(3)a=30°.
 a;(2)△ABE是等边三角形(证明见解析);(3)a=30°.
a;(2)△ABE是等边三角形(证明见解析);(3)a=30°.试题分析:(1)在等腰三角形中,顶角和底角的关系是∠B=
 (180°-∠A),∵AB=AC,∴∠ABC=∠C, ∵∠BAC=
(180°-∠A),∵AB=AC,∴∠ABC=∠C, ∵∠BAC=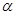 ,∴∠ABC=
,∴∠ABC= (180°-a),∴∠ABD=∠ABC -60°=30°-
(180°-a),∴∠ABD=∠ABC -60°=30°- a;(2)直观上看△ABE是等边三角形,而且有一个角是60°,只需要证明AB=BE即可,找到包含这两条线段的三角形△ABD和△BCE,故连接AD,CD,因为∠ABE=60°, ∠ABD=30°-
a;(2)直观上看△ABE是等边三角形,而且有一个角是60°,只需要证明AB=BE即可,找到包含这两条线段的三角形△ABD和△BCE,故连接AD,CD,因为∠ABE=60°, ∠ABD=30°- a,∠DBE=30°+
a,∠DBE=30°+ a,又因为∠DBC=60°,所以∠CBE=30°
a,又因为∠DBC=60°,所以∠CBE=30°-
 a=∠ABD,因为∠DBC=60°,BD=BC,所以△BDC是等边三角形,所以BD=CD,在△ABD和△ACD中,AB=AC,
a=∠ABD,因为∠DBC=60°,BD=BC,所以△BDC是等边三角形,所以BD=CD,在△ABD和△ACD中,AB=AC,BD=CD,AD=AD,所以△ABD≌△ACD,所以∠BAD=∠CAD=
 a,在△BCE中,∠BCE=150°,∠CBE=30°-
a,在△BCE中,∠BCE=150°,∠CBE=30°- a,∠BEC=
a,∠BEC= a=∠BAD,在△ABD和△CBE中, ∠BEC=∠BAD, ∠CBE=∠ABD,AB="AC" ,所以△ABD≌△CBE,所以AB=BE;(3)由(2)知△BDC是等边三角形,所以∠BCD=60°,因为∠BCE=150°,所以∠DCE=90°,因为∠DEC=45°,所以△DCE是等腰直角三角形,所以CD=CE=BC,在△BCE中, ∠BCE=150°,所以∠CBE=30°
a=∠BAD,在△ABD和△CBE中, ∠BEC=∠BAD, ∠CBE=∠ABD,AB="AC" ,所以△ABD≌△CBE,所以AB=BE;(3)由(2)知△BDC是等边三角形,所以∠BCD=60°,因为∠BCE=150°,所以∠DCE=90°,因为∠DEC=45°,所以△DCE是等腰直角三角形,所以CD=CE=BC,在△BCE中, ∠BCE=150°,所以∠CBE=30°-
 a=15°, 所以a=30°.
a=15°, 所以a=30°.试题解析:(1)∵AB=AC,
∴∠ABC=∠C,
∵∠BAC=
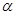 ,
,∴∠ABC=
 (180°-a),
(180°-a),∴∠ABD=∠ABC -60°=30°-
 a;
a;(2)故连接AD,CD,
∵∠ABE=60°, ∠ABD=30°-
 a,∠DBE=30°+
a,∠DBE=30°+ a,
a,又∵∠DBC=60°,
∴∠CBE=30°-
 a=∠ABD,
a=∠ABD,∵∠DBC=60°,BD=BC,
∴△BDC是等边三角形,
∴BD=CD,
在△ABD和△ACD中,AB=AC,BD=CD,AD=AD,
∴△ABD≌△ACD,
∴∠BAD=∠CAD=
 a,
a,在△BCE中,∠BCE=150°,∠CBE=30°-
 a,∠BEC=
a,∠BEC= a=∠BAD,
a=∠BAD,在△ABD和△CBE中, ∠BEC=∠BAD, ∠CBE=∠ABD,AB="AC" ,
∴△ABD≌△CBE,
∴AB=BE;
(3)由(2)知△BDC是等边三角形,
∴∠BCD=60°,
∵∠BCE=150°,
∴∠DCE=90°,
∵∠DEC=45°,
∴△DCE是等腰直角三角形,
∴CD=CE=BC,在△BCE中, ∠BCE=150°,
∴∠CBE=30°-
 a=15°,
a=15°, ∴a=30°.

练习册系列答案
相关题目