题目内容
 如图,BD是∠ABC的角平分线,DE⊥AB于E,△ABC的面积是36cm2,AB=BC=18cm,则DE=
如图,BD是∠ABC的角平分线,DE⊥AB于E,△ABC的面积是36cm2,AB=BC=18cm,则DE=考点:角平分线的性质
专题:
分析:过D作DF⊥BC于F,根据角平分线性质求出DE=DF,根据三角形的面积公式得出关于DE的方程,求出方程的解即可.
解答:
解:过D作DF⊥BC于F,
∵BD是∠ABC的角平分线,DE⊥AB,
∴DF=DE,
∵△ABC的面积是36cm2,AB=BC=18cm,
∴
×BC×DF+
×AB×DE=36,
∴
×18×DE+
×18×DE=36,
∴DE=2,
故答案为:2.

解:过D作DF⊥BC于F,
∵BD是∠ABC的角平分线,DE⊥AB,
∴DF=DE,
∵△ABC的面积是36cm2,AB=BC=18cm,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴DE=2,
故答案为:2.
点评:本题考查了三角形的面积,角平分线性质的应用,注意:角平分线上的点到角的两边的距离相等.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
在△ABC与△DEF中,AB=DF,AC=DE,CB=EF,那么( )
| A、△ABC≌△DEF |
| B、△ABC≌△DFE |
| C、△ABC≌△EDF |
| D、△ABC≌△EFD |
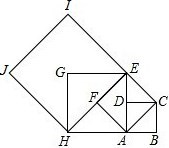 如图,四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去….
如图,四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去….