题目内容
解方程:|2x+1|-|x-2|=3.
考点:含绝对值符号的一元一次方程
专题:计算题
分析:解含绝对值符号的一元一次方程,要先去绝对值化为一元一次方程,所以分x≤-
或-
<x≤或x>2进行讨论,然后分别解一次方程确定原方程的解.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:当x≤-
时,原方程化为-2x-1+x-2=3,解得x=-6;
当-
<x≤2时,原方程化为2x+1+x-2=3,解得x=
;
当x>2时,原方程化为2x+1-(x-2)=3,解得x=0,不合题意舍去,
所以原方程的解为x=-6或x=
.
| 1 |
| 2 |
当-
| 1 |
| 2 |
| 4 |
| 3 |
当x>2时,原方程化为2x+1-(x-2)=3,解得x=0,不合题意舍去,
所以原方程的解为x=-6或x=
| 4 |
| 3 |
点评:本题考查了含绝对值符号的一元一次方程:解含绝对值符号的一元一次方程要根据绝对值的性质和绝对值符号内代数式的值分情况讨论,即去掉绝对值符号得到一般形式的一元一次方程,再求解.

练习册系列答案
相关题目
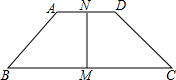 如图,AD∥BC,AB=CD,M是BC的中点,N是AD的中点,AD=5,BC=13,∠B+∠C=90°,求MN的长.
如图,AD∥BC,AB=CD,M是BC的中点,N是AD的中点,AD=5,BC=13,∠B+∠C=90°,求MN的长.