题目内容
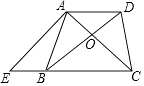
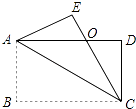
【题目】如图,已知梯形ABCD中,AD∥BC,AB=4,AD=3,AB⊥AC,AC平分∠DCB,过点DE∥AB,分别交AC、BC于F、E,设 ![]() =
= ![]() ,
, ![]() =
= ![]() .求:
.求: 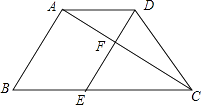
(1)向量 ![]() (用向量
(用向量 ![]() 、
、 ![]() 表示);
表示);
(2)tanB的值.
【答案】
(1)解:∵AD∥BC,
∴∠DAC=∠ACB,
∴AC平分∠DCB,
∴∠DCA=∠ACB,
∴∠DAC=∠DCA,
∴AD=DC,
∵DE∥AB,AB⊥AC,
∴DE⊥AC,
∴AF=CF,
∴BE=CE,
∵AD∥BC,DE∥AB,
∴四边形ABED是平行四边形,
∴DE=AB,
∴ ![]() =
= ![]() =
= ![]() ,
, ![]() =
= ![]()
![]() =
= ![]()
![]() ,
,
∴ ![]() =
= ![]() +
+ ![]()
![]() .
.
(2)解:∵∠DCF=∠ACB,∠DFC=∠BAC=90°,
∴△DFC∽△BAC,
∴ ![]() =
= ![]() =
= ![]() ,
,
∵CD=AD=3,∴BC=6,
在Rt△BAC中,∠BAC=90°,
∴AC= ![]() =
= ![]() =2
=2 ![]() ,
,
∴tanB= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)首先证明四边形ABED是平行四边形,推出DE=AB,推出 ![]() =
= ![]() =
= ![]() ,
, ![]() =
= ![]()
![]() =
= ![]()
![]() ,
, ![]() =
= ![]() +
+ ![]()
![]() .(2)由△DFC∽△BAC,推出
.(2)由△DFC∽△BAC,推出 ![]() =
= ![]() =
= ![]() ,求出BC,在Rt△BAC中,∠BAC=90°,根据AC=
,求出BC,在Rt△BAC中,∠BAC=90°,根据AC= ![]() =
= ![]() =2
=2 ![]() ,由tanB=
,由tanB= ![]() ,即可解决问题.
,即可解决问题.
【考点精析】根据题目的已知条件,利用梯形的定义和解直角三角形的相关知识可以得到问题的答案,需要掌握一组对边平行,另一组对边不平行的四边形是梯形.两腰相等的梯形是等腰梯形;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案【题目】如图,是某广场台阶(结合轮椅专用坡道)景观设计的模型,以及该设计第一层的截面图,第一层有十级台阶,每级台阶的高为0.15米,宽为0.4米,轮椅专用坡道AB的顶端有一个宽2米的水平面BC;《城市道路与建筑物无障碍设计规范》第17条,新建轮椅专用坡道在不同坡度的情况下,坡道高度应符合以下表中的规定: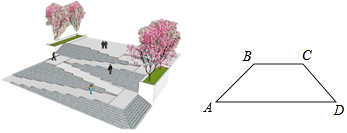
坡度 | 1:20 | 1:16 | 1:12 |
最大高度(米) | 1.50 | 1.00 | 0.75 |
(1)选择哪个坡度建设轮椅专用坡道AB是符合要求的?说明理由;
(2)求斜坡底部点A与台阶底部点D的水平距离AD.